题目内容
成都七中为绿化环境,移栽了银杏树2棵,梧桐树3棵。它们移栽后的成活率分别为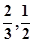 且每棵树是否存活互不影响,求移栽的5棵树中:
且每棵树是否存活互不影响,求移栽的5棵树中:
(1)银杏树都成活且梧桐树成活2棵的概率;
(2)成活的棵树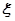 的分布列与期望.
的分布列与期望.
(1)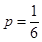 ;(2)
;(2)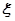 的分布列为:
的分布列为: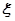
0 1 2 3 4 5 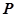

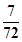


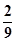

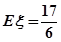
解析试题分析:(1) “银杏树都成活且梧桐树成活2棵”即“银杏树成活2棵”和 “梧桐树恰好成活2棵”这两个事件同时发生,因为这两个事件相互独立,所以独立事件同时发生的概率公式便可知,将这两个事件发生的概率相乘便得“银杏树都成活且梧桐树成活2棵”这个事件的概率;
(2)因为一共有5棵树,所以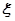 可能的取值为:
可能的取值为: .由概率公式求出
.由概率公式求出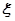 的各个取值的概率,便得其分布列及期望.
的各个取值的概率,便得其分布列及期望.
试题解析:(1)设 表示“银杏树都成活且梧桐树成活2棵”
表示“银杏树都成活且梧桐树成活2棵”
设 表示“银杏树成活
表示“银杏树成活 棵”;
棵”; ;
; ;
;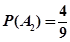
 表示“梧桐树成活
表示“梧桐树成活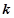 棵”;
棵”;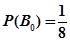 ;
;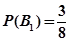 ;
; ;
; 3分
3分 5分
5分
(2)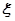 可能的取值:
可能的取值:
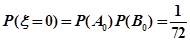
同理: ;
; ;
; ;
;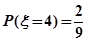
 7分
7分
∴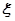 的分布列为:
的分布列为:
10分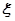
0 1 2 3 4 5 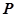

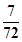


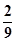

∴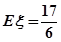 12分
12分
考点:1、古典概型;2、随机变量的分布列及其期望.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
| 品牌 | 甲 | 乙 | |||
| 首次出现故 障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
| 每辆利润 (万元) | 1 | 2 | 3 | 1.8 | 2.9 |
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率.
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列.
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(Ⅰ)求第2分钟末没有人买晚饭的概率;
(Ⅱ)估计第三个学生恰好等待4分钟开始买饭的概率.


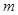 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求
 ,
,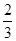 ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.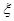 ,求
,求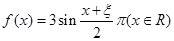 是偶函数”为事件D,求事件D发生的概率.
是偶函数”为事件D,求事件D发生的概率.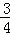 、
、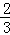 、
、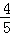 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
 的值;
的值;