题目内容
将一颗骰子先后抛掷2次,观察向上的点数,求:
(Ⅰ)两数之和为5的概率;
(Ⅱ)两数中至少有一个为奇数的概率.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)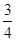 .
.
解析试题分析:(Ⅰ)通过列举可发现此问题中含有36个基本事件,而两数之和为5的有(1,4)、(4,1)、(2.3)、(3、2)4种,利用古典概型概率计算公式可得概率为 ;(Ⅱ)求出对立面的概率:对立面含的基本事件为(2,2)、(4,4)、(6,6)、(2,4)、(4,2)、(2,6)、(6,2)、(4,6)、(6、4)共9种,所以所求的概率为
;(Ⅱ)求出对立面的概率:对立面含的基本事件为(2,2)、(4,4)、(6,6)、(2,4)、(4,2)、(2,6)、(6,2)、(4,6)、(6、4)共9种,所以所求的概率为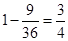 .
.
试题解析:将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件.
(Ⅰ)记“两数之和为5”为事件A,则事件A中含有4个基本事件,所以
P(A)= =
= .
.
答:两数之和为5的概率为 . 6分
. 6分
(Ⅱ)记“两数中至少有一个为奇数”为事件B,则事件B与“两数均为偶数”为对立事件,所以P(B)=1-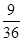 =
=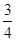 .
.
答:两数中至少有一个为奇数的概率为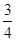 . 12分
. 12分
考点:古典概型概率的计算.

练习册系列答案
相关题目
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:
| 视力数据 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
| 人数 | | | | | 2 | | 2 | | 2 | 1 | | 1 | | |
(2)已知其余五个班学生视力的平均值分别为
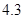 、
、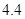 、
、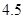 、
、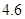 、
、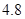 .若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于
.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于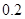 的概率.
的概率. 
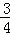 、
、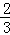 、
、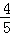 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.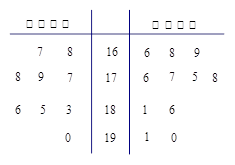
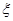 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出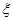 ,求随机变量
,求随机变量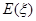 .
.
 的值;
的值;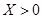 就去打球;若
就去打球;若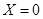 就去唱歌;若
就去唱歌;若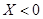 就去下棋.
就去下棋.