题目内容
5．设α，β是方程x2-2mx+2-m=0（x∈R）的两个实根，则α2+β2的最小值为（ ）| A． | 2 | B． | 0 | C． | 16 | D． | -$\frac{17}{4}$ |
分析 根据二次方程根与系数的关系，可得α+β=2m，αβ=2-m，且△=4m2+4m-8≥0，即m≤-2，或m≥1，构造函数y=α2+β2=（α+β）2-2αβ=4m2+2m-4，结合二次函数的图象和性质，可得答案．
解答 解：∵α，β是方程x2-2mx+2-m=0，
故α+β=2m，αβ=2-m，且△=4m2+4m-8≥0，即m≤-2，或m≥1，
则α2+β2=（α+β）2-2αβ=4m2+2m-4，
由y=4m2+2m-4的图象是开口朝上，且以m=$-\frac{1}{4}$为对称轴的抛物线，
故当m=1时，取最小值2，
故选：A．
点评 本题考查的知识点是二次函数的性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
相关题目
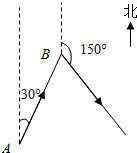如图所示，已知A、B两点的距离为100海里，B在A的北偏东30°处，甲船自A以50海里/小时的速度向B航行，同时乙船自B以30海里/小时的速度沿方位角150°方向航行．问航行几小时两船之间的距离最短？
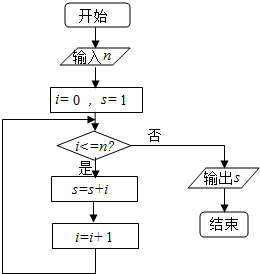执行如图所示的程序框图，若输入自然数n的值为6，则输出s的值是22．
10．某工人生产合格零售的产量逐月增长，前5个月的产量如表所示：
（I）若从这5组数据中抽出两组，求抽出的2组数据恰好是相邻的两个月数据的概率；
（Ⅱ）请根据所给5组数据，求出 y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；并根据线性回归方程预测该工人第6个月生产的合格零件的件数．
（附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 合格零件y（件） | 50 | 60 | 70 | 80 | 100 |
（Ⅱ）请根据所给5组数据，求出 y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；并根据线性回归方程预测该工人第6个月生产的合格零件的件数．
（附：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）