题目内容
20.已知圆C的圆心在x轴上,并且过点A(-1,1)和B(1,3),则圆的方程是(x-2)2+y2=10.分析 设圆心为M(a,0),由|MA|=|MB|求得a的值,可得圆心坐标以及半径的值,从而求得圆的方程.
解答 解:∵圆C的圆心在x轴上,设圆心为M(a,0),由圆过点A(-1,1)和B(1,3),
由|MA|=|MB|可得 MA2=MB2,即(a+1)2+1=(a-1)2+9,求得a=2,
可得圆心为M( 2,0),半径为|MA|=$\sqrt{{3}^{2}+1}$=$\sqrt{10}$,故圆的方程为 (x-2)2+y2=10,
故答案为:(x-2)2+y2=10.
点评 本题主要考查求圆的标准方程,求出圆心的坐标,是解题的关键,属于基础题.

练习册系列答案
相关题目
8.为了得到函数$y=\frac{1}{2}sin(2x+\frac{π}{3})$的图象,可以把函数$y=\frac{1}{2}sin2x$的图象上所有的点( )
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
5.设α,β是方程x2-2mx+2-m=0(x∈R)的两个实根,则α2+β2的最小值为( )
| A. | 2 | B. | 0 | C. | 16 | D. | -$\frac{17}{4}$ |
10.在空间直角坐标系中,以A(m,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰三角形,其中m∈Z,则m的值为( )
| A. | -4 | B. | 4 | C. | -6或4 | D. | 6或4 |
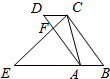 如图,四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于点F,∠ECA=∠D,求证:AC•BE=CE•AD.
如图,四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于点F,∠ECA=∠D,求证:AC•BE=CE•AD.