题目内容
(本题满分15分)
设抛物线M方程为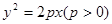 ,其焦点为F,P(
,其焦点为F,P(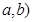 (
(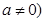 为直线
为直线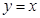 与抛物线M的一个交点,
与抛物线M的一个交点,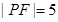
(1)求 抛物线的方程;
抛物线的方程;
(2)过焦点F的直线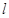 与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得
与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得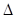 QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.
QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.
设抛物线M方程为
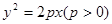 ,其焦点为F,P(
,其焦点为F,P(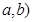 (
(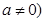 为直线
为直线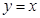 与抛物线M的一个交点,
与抛物线M的一个交点,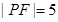
(1)求
 抛物线的方程;
抛物线的方程;(2)过焦点F的直线
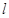 与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得
与抛物线交于A,B两点,试问在抛物线M的准线上是否存在一点Q,使得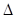 QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.
QAB为等边三角形,若存在求出Q点的坐标,若不存在请说明理由.解:(1)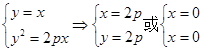 (舍去)
(舍去)

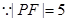
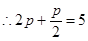
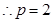
 --5分
--5分
(2)若直线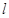 的斜率不存在,则Q只可能为
的斜率不存在,则Q只可能为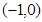 ,此时
,此时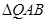 不是等边三角形,舍去,--7分
不是等边三角形,舍去,--7分
若直线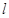 的斜率存在,设直线
的斜率存在,设直线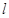 的方程为
的方程为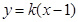 (
(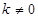 ),设直线
),设直线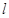 与抛物线的交点坐标为A(
与抛物线的交点坐标为A(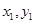 )、B(
)、B(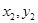 )
)
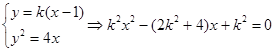 ,
,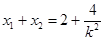
设存在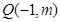 ,
,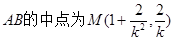 ,设Q到直线
,设Q到直线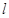 的距离为
的距离为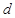
有题意可知:
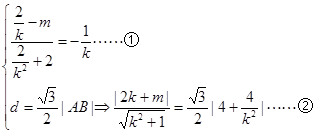 ---10分
---10分
由①可得: ------③
------③
③代入②得: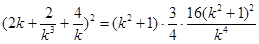 ,
,
化简得: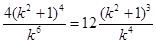
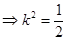 ----14分,
----14分,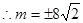
 为所求点-----15分
为所求点-----15分
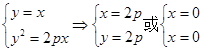 (舍去)
(舍去)
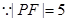
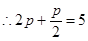
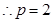
 --5分
--5分(2)若直线
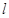 的斜率不存在,则Q只可能为
的斜率不存在,则Q只可能为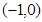 ,此时
,此时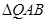 不是等边三角形,舍去,--7分
不是等边三角形,舍去,--7分若直线
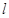 的斜率存在,设直线
的斜率存在,设直线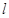 的方程为
的方程为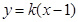 (
(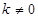 ),设直线
),设直线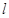 与抛物线的交点坐标为A(
与抛物线的交点坐标为A(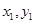 )、B(
)、B(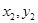 )
)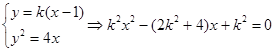 ,
,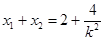
设存在
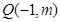 ,
,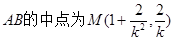 ,设Q到直线
,设Q到直线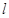 的距离为
的距离为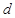
有题意可知:
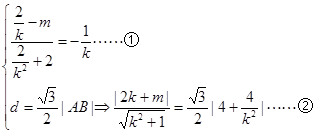 ---10分
---10分由①可得:
 ------③
------③③代入②得:
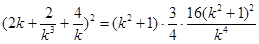 ,
,化简得:
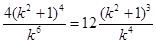
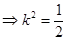 ----14分,
----14分,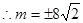
 为所求点-----15分
为所求点-----15分略

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 的线段AB的两个端点A、B都在抛物线
的线段AB的两个端点A、B都在抛物线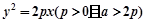 上滑动,则线段AB的中点M到
上滑动,则线段AB的中点M到 轴的最短距离是
轴的最短距离是 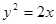 内一点A(1,1)作弦BC,若A为BC的中点,则直线BC的方程为
内一点A(1,1)作弦BC,若A为BC的中点,则直线BC的方程为 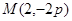 作抛物线
作抛物线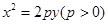 的两条切线,切点分别为
的两条切线,切点分别为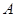 、
、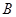 ,若
,若 中点的纵坐标为6,则抛物线的方程为 .
中点的纵坐标为6,则抛物线的方程为 .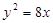 ,双曲线的右焦点是抛物线的焦点,离心率为2,则双曲线的标准方程是 .
,双曲线的右焦点是抛物线的焦点,离心率为2,则双曲线的标准方程是 . 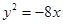 上一点,设P到此抛物线准线的距离是
上一点,设P到此抛物线准线的距离是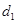 ,到直线
,到直线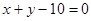 的距离是
的距离是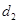 ,则
,则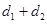 的最小值是
的最小值是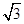
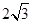
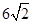
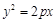 (
(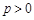 )焦点F的直线l和y轴正半轴交于点A,并且l与C在第一象限内的交点M恰好为A、F的中点,则直线的斜率
)焦点F的直线l和y轴正半轴交于点A,并且l与C在第一象限内的交点M恰好为A、F的中点,则直线的斜率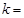 _____________。
_____________。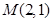 是抛物线
是抛物线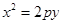 上的点,则以点
上的点,则以点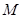 为切点的抛物线的切线方程为
为切点的抛物线的切线方程为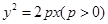 上一点M(1,m) (m>0)到其焦点的距离为5,双曲线
上一点M(1,m) (m>0)到其焦点的距离为5,双曲线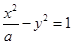 的左顶点为A.若双曲线的一条渐近线与直线AM平行,则实数
的左顶点为A.若双曲线的一条渐近线与直线AM平行,则实数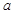 等于 .
等于 .