题目内容
3.如图,已知l1∥l2,AF:FB=2:5,BC:CD=4:1,则$\frac{AE}{EC}$=( )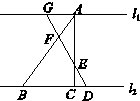
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由直线l1∥l2,根据平行线分线段成比例定理,即可得AF:FB=AG:BD=2:5,AE:EC=AG:CD,又由BC:CD=4:1,根据比例的性质,即可求得答案.
解答 解:∵直线l1∥l2,
∴AF:FB=AG:BD=2:5,AE:EC=AG:CD,
∵BC:CD=4:1
∴AG:CD=2:1,
∴AE:EC=2:1.
故选:A.
点评 此题考查了平行线分线段成比例定理.此题比较简单,解题的关键是注意比例线段的对应关系与比例的性质.

练习册系列答案
相关题目
15. 如图,正方形ABCD的边长为1,P,Q分别为AB,DA上的点.当△APQ的周长为2时,则∠PCQ的大小为( )
如图,正方形ABCD的边长为1,P,Q分别为AB,DA上的点.当△APQ的周长为2时,则∠PCQ的大小为( )
 如图,正方形ABCD的边长为1,P,Q分别为AB,DA上的点.当△APQ的周长为2时,则∠PCQ的大小为( )
如图,正方形ABCD的边长为1,P,Q分别为AB,DA上的点.当△APQ的周长为2时,则∠PCQ的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
13.过点(2,1)且与原点距离最大的直线的方程是( )
| A. | x+2y-5=0 | B. | y=$\frac{1}{2}$x+1 | C. | 2x+y-5=0 | D. | 3x+y-5=0 |
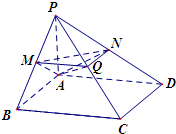 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,∠BAD=120°且PA⊥面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,∠BAD=120°且PA⊥面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点. 如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+φ)(A>0,ω>0,φ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧$\widehat{DE}$.
如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+φ)(A>0,ω>0,φ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧$\widehat{DE}$.