题目内容
14．函数f（x）=sinx在区间（0，2π）上可找到n个不同数x1，x2，…，xn，使得$\frac{f（{x}_{1}）}{{x}_{1}}$=$\frac{f（{x}_{2}）}{{x}_{2}}$=…=$\frac{f（{x}_{n}）}{{x}_{n}}$，则n的最大值等于（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 6 |
分析 设$\frac{f（{x}_{1}）}{{x}_{1}}$=$\frac{f（{x}_{2}）}{{x}_{2}}$=…=$\frac{f（{x}_{n}）}{{x}_{n}}$=k，则条件等价为f（x）=kx在区间（0，2π）上的根的个数，作出函数f（x）和y=kx的图象，数形结合可得结论．
解答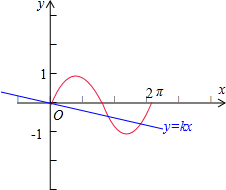 
解：设$\frac{f（{x}_{1}）}{{x}_{1}}$=$\frac{f（{x}_{2}）}{{x}_{2}}$=…=$\frac{f（{x}_{n}）}{{x}_{n}}$=k，则条件等价为f（x）=kx在区间（0，2π）上的根的个数，
作出函数f（x）和y=kx的图象，
由图象可知y=kx与函数f（x）在区间（0，2π）上的交点个数最多为2，
故选：B．
点评 本题主要考查函数交点个数的应用，利用数形结合是解决本题的关键，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
9．设集合A={x|x≤2}，则下列四个关系中正确的是（ ）
| A． | 1∈A | B． | 1∉A | C． | {1}∈A | D． | 1⊆A |
19．已知sinα=$\frac{{\sqrt{5}}}{5}$，sinβ=$\frac{{\sqrt{10}}}{10}$，且α，β均为锐角，则α+β的值为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{3π}{4}$ | C． | $\frac{π}{4}$或$\frac{3π}{4}$ | D． | $\frac{π}{2}$ |
