题目内容
【题目】已知函数![]() .
.
(1)求![]() 的极值;
的极值;
(2)若![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)极大值为![]() ;
;![]() 的极小值为
的极小值为![]() ;(2)见解析
;(2)见解析
【解析】
(1)求导求出![]() ,求出单调区间,进而求出极值;
,求出单调区间,进而求出极值;
(2)由(1)![]() ,结合极值点考虑
,结合极值点考虑![]() 与
与![]() 的大小关系,
的大小关系,![]() 在
在![]() 为减函数,只需比较
为减函数,只需比较![]() 与
与![]() 大小关系,而
大小关系,而![]() ,转化为比较
,转化为比较![]() 与
与![]() 比较大小,构造函数
比较大小,构造函数![]() ,
,![]() ,通过求导求出
,通过求导求出![]() 的单调性,即可得出
的单调性,即可得出![]() 的不等量关系,同理构造函数
的不等量关系,同理构造函数![]() ,得出
,得出![]() 的不等量关系,即可证明结论.
的不等量关系,即可证明结论.
(1)解:因为![]() ,
,
所以![]() ,
,
所以当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
则![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
故![]() 的极大值为
的极大值为![]() ;
;
![]() 的极小值为
的极小值为![]() .
.
(2)证明:由(1)知![]() .
.
设函数![]() ,
,![]() ,
,
![]()
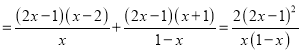 ,
,
则![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递增,
上单调递增,
故![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
因为![]() ,所以
,所以![]() .
.
因为![]() ,且
,且![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() .①
.①
设函数![]() ,
,![]() ,
,
![]()
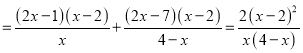 ,
,
则![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递增,
上单调递增,
故![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
因为![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,且
,且![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .②
.②
结合①②,可得![]() .
.

【题目】近来天气变化无常,陡然升温、降温幅度大于![]() 的天气现象出现增多.陡然降温幅度大于
的天气现象出现增多.陡然降温幅度大于![]() 容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的
容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的![]() 名幼儿进行调查,得到了如下的列联表,若在全部
名幼儿进行调查,得到了如下的列联表,若在全部![]() 名幼儿中随机抽取
名幼儿中随机抽取![]() 人,抽到患伤风感冒疾病的幼儿的概率为
人,抽到患伤风感冒疾病的幼儿的概率为![]() ,
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过![]() 的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的![]() 名女性幼儿中,有
名女性幼儿中,有![]() 名又患黄痘病.现在从患伤风感冒疾病的
名又患黄痘病.现在从患伤风感冒疾病的![]() 名女性中,选出
名女性中,选出![]() 名进行其他方面的排查,记选出患黄痘病的女性人数为
名进行其他方面的排查,记选出患黄痘病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: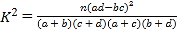 ,其中
,其中![]()
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间![]() ,结果如下:
,结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间 | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分种开始准备第三位顾客的泡茶工具的概率;
(2)用![]() 表示至第4分钟末已准备好了工具的顾客人数,求
表示至第4分钟末已准备好了工具的顾客人数,求![]() 的分布列及数学期望.
的分布列及数学期望.