题目内容
【题目】命题![]() :已知实数
:已知实数![]() ,
, ![]() 满足约束条件
满足约束条件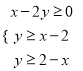 ,二元一次不等式
,二元一次不等式![]() 恒成立,
恒成立,
命题![]() :设数列
:设数列![]() 的通项公式为
的通项公式为![]() ,若
,若![]() ,使得
,使得![]() .
.
(1)分别求出使命题![]() ,
, ![]() 为真时,实数
为真时,实数![]() 的取值范围;
的取值范围;
(2)若命题![]() 与
与![]() 真假相同,求实数
真假相同,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() 或
或![]()
【解析】试题分析:
(1)由题意,画出可行域,结合图象得到当目标函数过点![]() 时,目标函数取得最大值,联立方程组,求解点
时,目标函数取得最大值,联立方程组,求解点![]() 的坐标,代入求解最大值,得出
的坐标,代入求解最大值,得出![]() 范围,再由基本不等式,看求解
范围,再由基本不等式,看求解![]() 为真时
为真时![]() 的范围即可.
的范围即可.
(2)因为命题![]() 与
与![]() 真假相同,分类讨论,即可求解
真假相同,分类讨论,即可求解![]() 的取值范围.
的取值范围.
试题解析:
(1)约束条件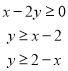 ,画出可行域,结合图象可得
,画出可行域,结合图象可得
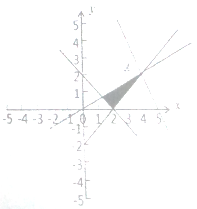
当目标函数![]() 过点
过点![]() 时,目标函数取得最大值.
时,目标函数取得最大值.
![]() 得
得![]() ,则
,则![]() 的最大值为
的最大值为![]() .所以命题
.所以命题![]() 为真:
为真: ![]()
由![]()
![]() (当且仅当
(当且仅当![]() ,即
,即![]() 时取等号.)
时取等号.)
所以命题![]() 为真:
为真: ![]()
(2)因为命题![]() 与
与![]() 真假相同
真假相同
①若![]() 与
与![]() 同为真:则
同为真:则![]() ,∴
,∴![]() ,②若
,②若![]() 与
与![]() 同为假,则
同为假,则![]() ,∴
,∴![]() .
.
综上: ![]() 或
或![]() .
.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目