Question

【题目】某纺纱厂生产甲、乙两种棉纱，已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨；生产乙种棉纱1吨需耗一级籽棉1吨，二级籽棉2吨.每1吨甲种棉纱的利润为900元，每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中，要求消耗一级籽棉不超过250吨，二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨，能使利润总额最大？并求出利润总额的最大值.

Answer 1

【答案】当过点M（，），利润总额z＝900x＋600y取最大值130000元.

【解析】

试题分析：解：设生产甲、乙两种棉纱分别为x、y吨，利润总额为z，

则z＝900x＋600y 2

且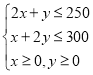 4

作出以上不等式组所表示的平面区域（如图），

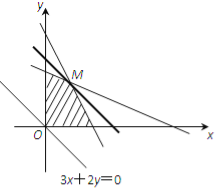
即可行域. 6

作直线l：900x＋600y＝0，即3x＋2y＝0，

把直线l向右上方平移至过直线2x＋y＝250与

直线x＋2y＝300的交点位置M（，）， 10

此时所求利润总额z＝900x＋600y取最大值130000元. 12