题目内容
已知数列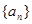 满足
满足 (
( ).
).
(1)若数列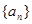 是等差数列,求它的首项和公差;
是等差数列,求它的首项和公差;
(2)证明:数列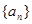 不可能是等比数列;
不可能是等比数列;
(3)若 ,
, (
( ),试求实数
),试求实数 和
和 的值,使得数列
的值,使得数列 为等比数列;并求此时数列
为等比数列;并求此时数列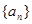 的通项公式.
的通项公式.
(1)首项为 ,公差为
,公差为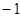 ,(2)详见解析,(3)
,(2)详见解析,(3)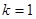 ,
, ,
, .
.
解析试题分析:(1)求特殊数列(等差数列或等比数列)通项的基本方法就是待定系数法.本题中只需确定公差与首项,即只需列出两个独立条件就可解出. 由已知 ,
, ,若
,若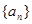 是等差数列,则
是等差数列,则 ,即
,即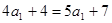 ,得
,得 ,
, , 故
, 故 .所以,数列
.所以,数列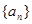 的首项为
的首项为 ,公差为
,公差为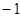 .(2)证明数列
.(2)证明数列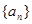 不可能是等比数列,宜从反面出发推出矛盾即可. 假设数列
不可能是等比数列,宜从反面出发推出矛盾即可. 假设数列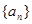 是等比数列,则有
是等比数列,则有 ,解得
,解得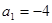 ,从而
,从而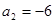 ,
,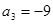 ,又
,又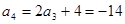 .
. ,
,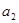 ,
,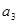 ,
, 不成等比数列,与假设矛盾,(3)本题也可同(1)一样用待定系数法解,即需列出三个独立条件,解出参数
不成等比数列,与假设矛盾,(3)本题也可同(1)一样用待定系数法解,即需列出三个独立条件,解出参数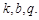 但运算量较大,故考虑用方程恒等,系数对应相等方法求解. 由
但运算量较大,故考虑用方程恒等,系数对应相等方法求解. 由 化简得
化简得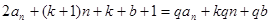 ,所以,
,所以,
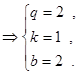 再由数列
再由数列 通项可得
通项可得 .
.
试题解析:解(1)由已知 ,
, ,
,
若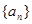 是等差数列,则
是等差数列,则 ,即
,即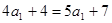 ,
,
得 ,
, , 故
, 故 .
.
所以,数列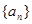 的首项为
的首项为 ,公差为
,公差为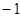 . (5分)
. (5分)
(2)假设数列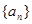 是等比数列,则有
是等比数列,则有 ,
,
即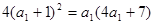 ,
,
解得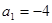 ,从而
,从而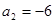 ,
,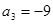 ,
,
又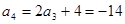 .
.
因为 ,
,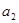 ,
,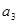 ,
, 不成等比数列,与假设矛盾,
不成等比数列,与假设矛盾,
所以数列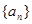 不是等比数列. (10分)
不是等比数列. (10分)
(3)由题意,对任意 ,有
,有 (
( 为定值且
为定值且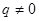 ),
),
即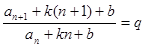 .
.
即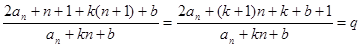 ,
,
于是,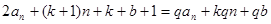 ,
,
所以,
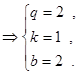
所以,当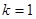 ,
, 时,数列
时,数列 为等比数列.
为等比数列.
此数列的首项为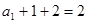 ,公比为
,公比为 ,所以
,所以
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
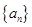 满足
满足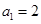 ,向量
,向量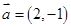 ,
,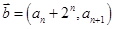 且
且 .
.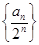 为等差数列,并求
为等差数列,并求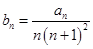 ,若对任意
,若对任意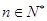 都有
都有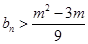 成立,求实数
成立,求实数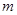 的取值范围.
的取值范围.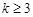 ,若项数为
,若项数为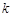 的数列
的数列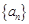 满足:对任意的
满足:对任意的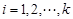 ,均有
,均有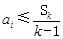 (其中
(其中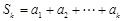 ),则称数列
),则称数列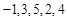 和
和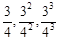 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由;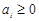 对
对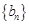 是公差为
是公差为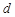 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数 ,
,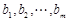
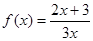 , 数列
, 数列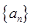 满足
满足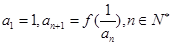 .
. ,若
,若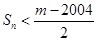 对一切
对一切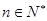 成立,求最小正整数m.
成立,求最小正整数m.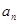 }、{
}、{  }满足:
}满足: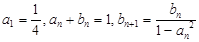 .
.
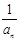 }为等差数列,并求数列
}为等差数列,并求数列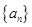 和{
和{  ,求实数
,求实数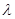 为何值时
为何值时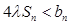 恒成立.
恒成立.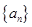 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列,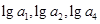 成等差数列,又
成等差数列,又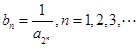 .
.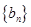 为等比数列;
为等比数列;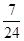 ,求数列
,求数列 为数列
为数列 的前
的前 项和,求
项和,求 是首项为a,公差为d的等差数列
是首项为a,公差为d的等差数列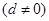 ,
, 是其前n项的和。记
是其前n项的和。记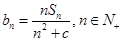 ,其中c为实数。
,其中c为实数。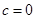 ,且
,且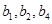 成等比数列,证明:
成等比数列,证明: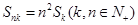 ;
;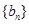 是等差数列,证明:
是等差数列,证明: 的前n项和为
的前n项和为 ,
,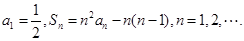
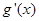 ;
;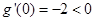 ,求证:
,求证: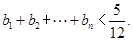
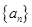 中,
中,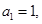 且对任意的
且对任意的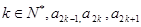 成等比数列,其公比为
成等比数列,其公比为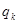 ,
,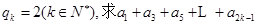 ;
;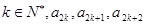 成等差数列,其公差为
成等差数列,其公差为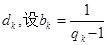 .
.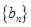 成等差数列,并指出其公差;
成等差数列,并指出其公差;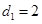 ,试求数列
,试求数列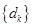 的前
的前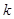 项和
项和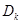 .
.