题目内容
(本小题满分12分)甲、乙等 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为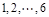 ).
).
(Ⅰ)求甲、乙两考生的面试序号至少有一个为奇数的概率;
(Ⅱ)记在甲、乙两考生之间参加面试的考生人数为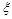 ,求随机变量
,求随机变量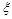 的分布列与期望.
的分布列与期望.
(Ⅰ)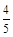 ;(Ⅱ)分布列是:
;(Ⅱ)分布列是: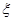
0 1 2 3 4 P 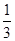
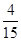
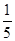
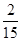
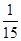
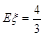 .
.
解析试题分析:(Ⅰ)用组合计算基本事件数,由等可能性事件的概率计算公式即可求解;(Ⅱ)利用组合也可以求出随机变量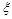 的分布列,然后根据期望的定义求出
的分布列,然后根据期望的定义求出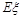 .
.
(Ⅰ)只考虑甲、乙两考生的相对位置,用组合计算基本事件数;
设A表示“甲、乙的面试序号至少有一个为奇数”,则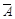 表示“甲、乙的序号均为偶数”,
表示“甲、乙的序号均为偶数”,
由等可能性事件的概率计算公式得: 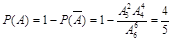
甲、乙两考生的面试序号至少有一个为奇数的概率是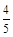 . 6分
. 6分
(另解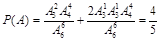 )
)
(Ⅱ)随机变量 的所有可能取值是0,1,2,3,4,
的所有可能取值是0,1,2,3,4,
且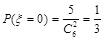 ,
,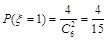 ,
,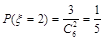 ,
,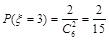 ,
,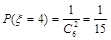
[另解: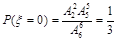 ,
,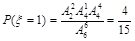 ,
,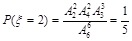 ,
,
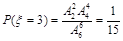 10分
10分
所以随机变量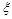 的分布列是:
的分布列是:
所以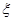
0 1 2 3 4 P 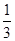
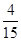
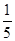
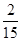
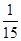
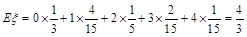 ,
,
即甲、乙两考生之间的面试考生个数 的期望值是
的期望值是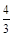 . 12分.
. 12分.
考点:概率知识,分布列和期望的求法.

 名校课堂系列答案
名校课堂系列答案某种产品按质量标准分为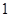 ,
, ,
,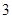 ,
,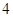 ,
,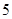 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
| 等级 | 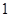 |  | 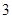 | 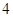 | 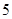 |
| 频率 | 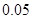 | 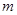 | 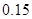 | 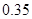 | 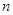 |
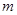 ,
,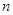 ;
;(2)在(1)的条件下,从等级为3和5的所有产品中,任意抽取2个,求抽取的2个产品等级恰好相同的概率.
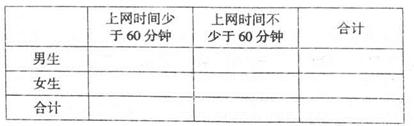
某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
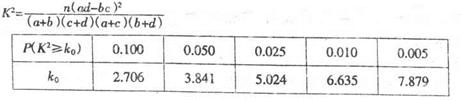
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记抽取的3 个成绩中语文,外语两科成绩至少有一科优秀的个数为X ,求X的分布列和期望E(x).
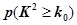 | 0.010 | 0.005 | 0.001 |
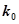 | 6.635 | 7.879 | 10.828 |
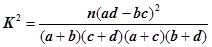
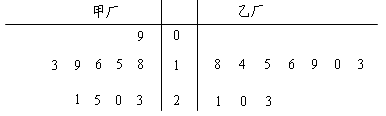
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 105 |
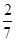
(Ⅰ)请完成上面的列联表;
(Ⅱ)从105名学生中选出10名学生组成参观团,若采用下面的方法选取:用简单随机抽样从105人中剔除5人,剩下的100人再按系统抽样的方法抽取10人,请写出在105人中,每人入选的概率(不必写过程);
(Ⅲ)把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到6号或10号的概率.
 的分布列及其数学期望
的分布列及其数学期望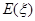 ;
;

 •
•
 ,获得50元奖金的概率为
,获得50元奖金的概率为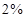 .
.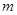 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为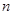 ,求
,求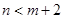 的概率.
的概率.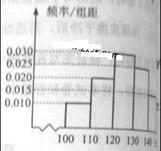
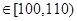 ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110 ,求T的数学期望.
,求T的数学期望.