题目内容
18.已知函数f(x)=x2-ax,g(x)=b+aln(x-1),存在实数a(a≥1),使y=f(x)的图象与y=g(x)的图象无公共点,则实数b的取值范围为( )| A. | [1,+∞) | B. | [1,$\frac{3}{4}+ln2$) | C. | [$\frac{3}{4}+ln2,+∞$) | D. | (-$∞,\frac{3}{4}+ln2$) |
分析 若y=f(x)的图象与y=g(x)的图象无公共点,则等价为f(x)-g(x)>0或f(x)-g(x)<0恒成立,利用参数分离法,转化为求函数的最值,构造函数,求函数的导数,利用导数进行求解即可.
解答 解:若y=f(x)的图象与y=g(x)的图象无公共点,
则等价为f(x)-g(x)>0或f(x)-g(x)<0恒成立,
即x2-ax-b-aln(x-1)>0或,x2-ax-b-aln(x-1)<0恒成立,
即x2-ax-aln(x-1)>b或x2-ax-aln(x-1)<b恒成立,
设h(x)=x2-ax-aln(x-1),则函数h(x)的定义域为(1,+∞),
函数的导数h′(x)=2x-a-$\frac{a}{x-1}$=$\frac{2x(x-\frac{a+2}{2})}{x-1}$,
当a≥1时,$\frac{a+2}{2}$≥$\frac{3}{2}$,
故x∈(1,$\frac{a+2}{2}$)时,h′(x)<0,
x∈($\frac{a+2}{2}$,+∞)时,h′(x)>0,
即当x=$\frac{a+2}{2}$时,函数h(x)取得极小值同时也是最小值h($\frac{a+2}{2}$)=$-\frac{{a}^{2}}{4}+1-aln\frac{a}{2}$,
设G(a)=h($\frac{a+2}{2}$)=$-\frac{{a}^{2}}{4}+1-aln\frac{a}{2}$,
则G(a)在[1,+∞)上为减函数,
∴G(a)的最大值为G(1)=$\frac{3}{4}+ln2$,
故h(x)的最小值h($\frac{a+2}{2}$)≤$\frac{3}{4}+ln2$,
则若x2-ax-aln(x-1)>b,
则b<$\frac{3}{4}+ln2$,
若x2-ax-aln(x-1)<b恒成立,则不成立,
综上b<$\frac{3}{4}+ln2$,
故选:D
点评 本题主要考查函数的相交问题,构造函数,利用参数分类法,结合导数研究函数的最值是解决本题的关键.综合性较强,难度较大.

| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
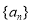 是等差数列,下列数列中仍为等差数列的有( )
是等差数列,下列数列中仍为等差数列的有( )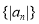 ;
;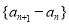 ;
;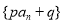 (
( ,
,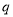 为常数);
为常数);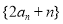 .
.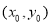 是直线
是直线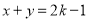 与圆
与圆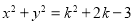 的公共点,则
的公共点,则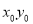 的取值范围是__________.
的取值范围是__________.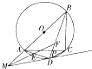 如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径.经过点D的圆的切线与BA的延长线交于点M.∠BMD的平分线分别交AD,BD于点E,FAC,BD交于点P.
如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径.经过点D的圆的切线与BA的延长线交于点M.∠BMD的平分线分别交AD,BD于点E,FAC,BD交于点P.