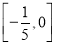题目内容
6.在平面直角坐标系xOy中,一动圆经过点($\frac{1}{2}$,0)且与直线x=-$\frac{1}{2}$相切,设该动圆圆心的轨迹为曲线E.(Ⅰ)求曲线E的方程;
(Ⅱ)设P是曲线E的动点,点B、C在y轴上,△PBC的内切圆的方程为(x-1)2+y2=1,求△PBC面积的最小值.
分析 (Ⅰ)运用抛物线的定义,可得轨迹为抛物线,进而得到方程;
(Ⅱ)设P(x0,y0),B(0,b),C(0,c),求得直线PB的方程,运用直线和圆相切的条件:d=r,求得b,c的关系,求得△PBC的面积,结合基本不等式,即可得到最小值.
解答 解:(Ⅰ)由题意可知圆心到($\frac{1}{2}$,0)的距离等于到直线x=-$\frac{1}{2}$的距离,
由抛物线的定义可知,圆心的轨迹方程:y2=2x.
(Ⅱ)设P(x0,y0),B(0,b),C(0,c),
直线PB的方程为:(y0-b)x-x0y+x0b=0,
又圆心(1,0)到PB的距离为1,
即$\frac{|{y}_{0}-b+{x}_{0}b|}{\sqrt{({y}_{0}-b)^{2}+{{x}_{0}}^{2}}}$=1,整理得:(x0-2)b2+2y0b-x0=0,
同理可得:(x0-2)c2+2y0c-x0=0,
所以,可知b,c是方程(x0-2)x2+2y0x-x0=0的两根,
所以b+c=$\frac{-2{y}_{0}}{{x}_{0}-2}$,bc=$\frac{-{x}_{0}}{{x}_{0}-2}$,
依题意bc<0,即x0>2,
则(c-b)2=$\frac{4{{x}_{0}}^{2}+4{{y}_{0}}^{2}-8{x}_{0}}{({x}_{0}-2)^{2}}$,
因为y02=2x0,所以:|b-c|=|$\frac{2{x}_{0}}{{x}_{0}-2}$|
所以S=$\frac{1}{2}$|b-c|•|x0|=(x0-2)+$\frac{4}{{x}_{0}-2}$+4≥8
当x0=4时上式取得等号,
所以△PBC面积最小值为8.
点评 本题考查抛物线的定义、方程和性质,主要考查定义法和方程的运用,同时考查直线和圆相切的条件:d=r,考查化简整理的运算能力,属于中档题.

| A. | (1,2] | B. | [1,2] | C. | (-∞,-3)∪(1,+∞) | D. | [1,2) |
| A. | [1,+∞) | B. | [1,$\frac{3}{4}+ln2$) | C. | [$\frac{3}{4}+ln2,+∞$) | D. | (-$∞,\frac{3}{4}+ln2$) |
| A. | -log32 | B. | log32 | C. | -log23 | D. | log23 |
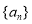 中,
中,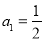 ,
,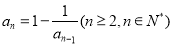 .
.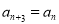 ;
;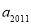 .
.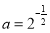 ,
,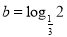 ,
, ,则( )
,则( )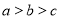 B.
B.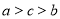
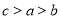 D.
D.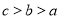
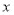 ,
, 满足不等式组
满足不等式组 时,
时,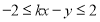 恒成立,则实数
恒成立,则实数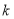 的取值范围是( )
的取值范围是( )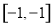 B.
B.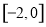
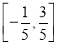 D.
D.