题目内容
6.设函数f(x)=|3x-1|+ax+3.(1)若a=1,解不等式f(x)≤5;
(2)若函数f(x)有最小值,求实数a的取值范围.
分析 (Ⅰ)a=1时,f(x)=|3x-1|+x+3,分类讨论,去掉绝对值,求得x的范围.
(Ⅱ)化简f(x)的解析式,根据一次函数的单调性与一次项系数符号的关系,求得a的范围.
解答 解:(Ⅰ)a=1时,f(x)=|3x-1|+x+3.
当$x≥\frac{1}{3}$时,f(x)≤5可化为3x-1+x+3≤5,解之得$\frac{1}{3}≤x≤\frac{3}{4}$;
当$x<\frac{1}{3}$时,f(x)≤5可化为-3x+1+x+3≤5,解之得$-\frac{1}{2}≤x<\frac{1}{3}$.
综上可得,原不等式的解集为$\{x|-\frac{1}{2}≤x≤\frac{3}{4}\}$.
(Ⅱ)$f(x)=|3x-1|+ax+3=\left\{\begin{array}{l}(3+a)x+2,(x≥\frac{1}{3})\\(a-3)x+4.(x<\frac{1}{3})\end{array}\right.$
函数f(x)有最小值的充要条件为$\left\{\begin{array}{l}3+a≥0\\ a-3≤0\end{array}\right.$,即-3≤a≤3.
点评 本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
18.已知函数f(x)=x2-ax,g(x)=b+aln(x-1),存在实数a(a≥1),使y=f(x)的图象与y=g(x)的图象无公共点,则实数b的取值范围为( )
| A. | [1,+∞) | B. | [1,$\frac{3}{4}+ln2$) | C. | [$\frac{3}{4}+ln2,+∞$) | D. | (-$∞,\frac{3}{4}+ln2$) |
18.已知向量$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,定义:cλ=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$,其中0≤λ≤1.若${c_λ}•{c_{\frac{1}{2}}}=\frac{1}{2}$,则|cλ|的值不可能为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
10.如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )?
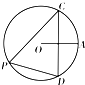

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.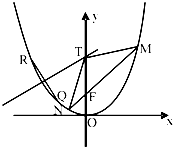 如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.
如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.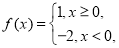 ,若
,若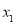 ,
, 均满足不等式
均满足不等式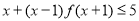 ,则
,则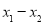 的最大值为__________.
的最大值为__________.