题目内容
(本题满分12分)
已知四棱锥P—ABCD中,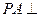 平面ABCD,底面ABCD为菱形,
平面ABCD,底面ABCD为菱形,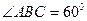 ,AB=PA=2,E.F分别为BC.PD的中点。
,AB=PA=2,E.F分别为BC.PD的中点。
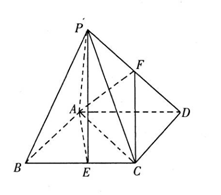
(Ⅰ)求证:PB//平面AFC;
(Ⅱ)求平面PAE与平面PCD所成锐二面角的余弦值。
已知四棱锥P—ABCD中,
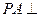 平面ABCD,底面ABCD为菱形,
平面ABCD,底面ABCD为菱形,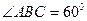 ,AB=PA=2,E.F分别为BC.PD的中点。
,AB=PA=2,E.F分别为BC.PD的中点。
(Ⅰ)求证:PB//平面AFC;
(Ⅱ)求平面PAE与平面PCD所成锐二面角的余弦值。
解析:(1)连结BD交AC于O,
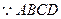 为菱形,则BO=OD…………1分
为菱形,则BO=OD…………1分
连结FO,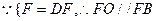 …………3分
…………3分
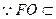 平面AFC,
平面AFC,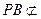 平面AFC,
平面AFC,
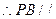 平面AFC…………4分
平面AFC…………4分
(2)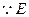 为BC中点,
为BC中点,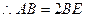
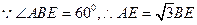
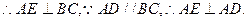 …………6分
…………6分
建立如图所示的空间直角坐标系,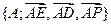 ,
,
则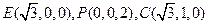 ,D(90,2,0)…………8分
,D(90,2,0)…………8分
平面PAE的一个法向量为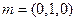 ……9分
……9分
设平面PDC的一个法向量为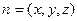
则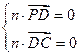
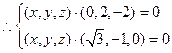
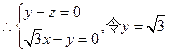
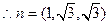 …………11分
…………11分
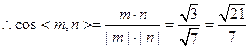
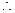 平面PAE与平面PCD所成锐二面角的余弦值为
平面PAE与平面PCD所成锐二面角的余弦值为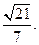 ……12分
……12分
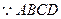 为菱形,则BO=OD…………1分
为菱形,则BO=OD…………1分连结FO,
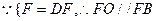 …………3分
…………3分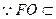 平面AFC,
平面AFC,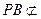 平面AFC,
平面AFC,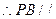 平面AFC…………4分
平面AFC…………4分(2)
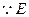 为BC中点,
为BC中点,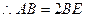
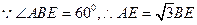
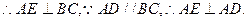 …………6分
…………6分建立如图所示的空间直角坐标系,
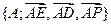 ,
,则
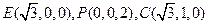 ,D(90,2,0)…………8分
,D(90,2,0)…………8分平面PAE的一个法向量为
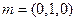 ……9分
……9分设平面PDC的一个法向量为
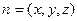
则
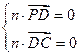
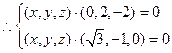
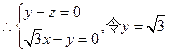
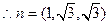 …………11分
…………11分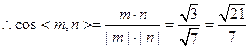
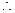 平面PAE与平面PCD所成锐二面角的余弦值为
平面PAE与平面PCD所成锐二面角的余弦值为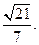 ……12分
……12分略

练习册系列答案
相关题目
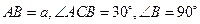 , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角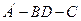 的大小记为
的大小记为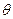 .
.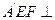 平面BCD;
平面BCD; 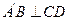 时,求
时,求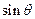 的值;
的值; 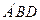 的距离.
的距离.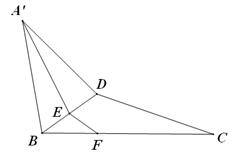
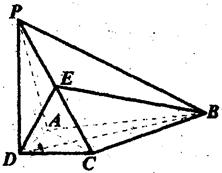 E为PC的中点,AD=CD=l,BC=PC,
E为PC的中点,AD=CD=l,BC=PC,
 杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由。
杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由。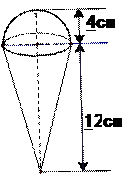
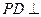 平面
平面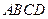 ,
,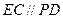 ,
,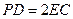 ,
, 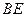 //平面
//平面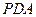 ;
;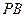 的中点,求证:
的中点,求证: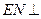 平面
平面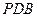 ;
;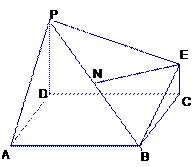
 底面ABCD,
底面ABCD,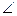 DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.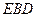 与平面
与平面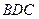 的夹角大于
的夹角大于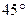 ,求k的取值范围.
,求k的取值范围.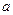 的正方体
的正方体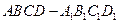 中,
中,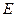 是线段
是线段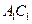 的中点,
的中点,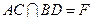 .
.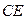 ^
^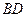 ;(Ⅱ) 求证:
;(Ⅱ) 求证: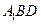 ;(Ⅲ) 求三棱锥
;(Ⅲ) 求三棱锥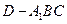 的体积.
的体积.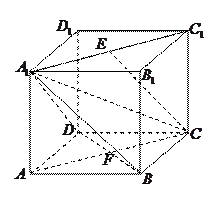
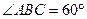 ,点M
,点M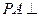 平面ABCD,AC、BD交于点O。
平面ABCD,AC、BD交于点O。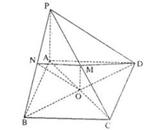
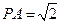 ,求证:AM
,求证:AM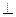 平面PBD;
平面PBD;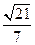 ,求PA的长
,求PA的长