题目内容
如图:在直角三角形ABC中,已知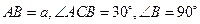 , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角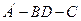 的大小记为
的大小记为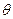 .
.
⑴求证:平面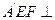 平面BCD;
平面BCD;
⑵当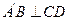 时,求
时,求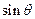 的值;
的值;
⑶在⑵的条件下,求点C到平面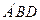 的距离.
的距离.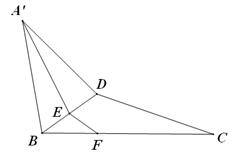
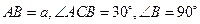 , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角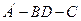 的大小记为
的大小记为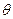 .
.⑴求证:平面
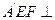 平面BCD;
平面BCD; ⑵当
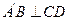 时,求
时,求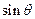 的值;
的值; ⑶在⑵的条件下,求点C到平面
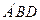 的距离.
的距离.
(1)证明:由△PBA为Rt△, ∠C=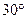 AB=
AB=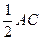
 ∵D为AC中点,
∵D为AC中点,
∴AD=BD=DC ∵△ABD为正三角形 又∵E为BD中点
∴BD⊥AE’ BD⊥EF 又由A’E EF=E,且A’E、EF
EF=E,且A’E、EF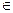 平面A’EF
平面A’EF
BD⊥平面A’EF ∴面A’EF⊥平面BCD………………………4分
(2) BD⊥AE’, BD⊥EF得
∠A’EF为二面角A’-BD-C的平面角的大小即∠A’EF=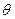 ……………5分
……………5分
以E为坐标原点,得
由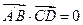 ,得
,得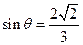 ………………10分
………………10分
(3)用等积法易得所求距离为: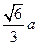 ………………14分
………………14分
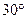 AB=
AB=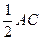
 ∵D为AC中点,
∵D为AC中点,∴AD=BD=DC ∵△ABD为正三角形 又∵E为BD中点
∴BD⊥AE’ BD⊥EF 又由A’E
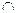 EF=E,且A’E、EF
EF=E,且A’E、EF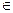 平面A’EF
平面A’EFBD⊥平面A’EF ∴面A’EF⊥平面BCD………………………4分
(2) BD⊥AE’, BD⊥EF得
∠A’EF为二面角A’-BD-C的平面角的大小即∠A’EF=
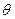 ……………5分
……………5分以E为坐标原点,得

由
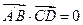 ,得
,得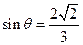 ………………10分
………………10分(3)用等积法易得所求距离为:
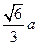 ………………14分
………………14分略

练习册系列答案
相关题目
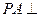 平面ABCD,底面ABCD为菱形,
平面ABCD,底面ABCD为菱形, ,AB=PA=2,E.F分别为BC.PD的中点。
,AB=PA=2,E.F分别为BC.PD的中点。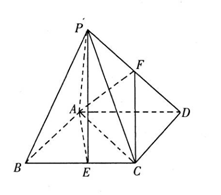
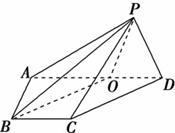
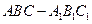 中,
中,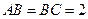 ,
,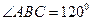 ,又顶点
,又顶点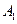 在底面
在底面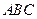 上的射影落在
上的射影落在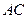 上,侧棱
上,侧棱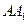 与底面
与底面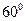 角,
角,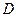 为
为
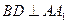 ;
;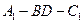 为直二面角,试求侧棱
为直二面角,试求侧棱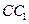 与侧面
与侧面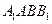 的距离.
的距离.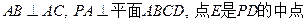

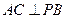
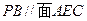
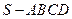 的底面是矩形,
的底面是矩形,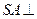 底面
底面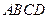 ,
,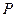 为
为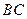 边的中点,
边的中点,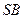 与平面
与平面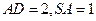 .
.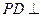 平面
平面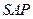 ;
;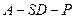 的余弦的大小.
的余弦的大小.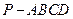 的底面
的底面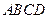 是一个边长为4的正方形,侧面
是一个边长为4的正方形,侧面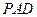 是正三角形,侧面
是正三角形,侧面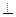 底面
底面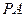 与平面
与平面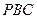 所成的角的正弦值。
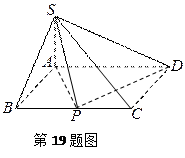
所成的角的正弦值。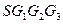 中,E、F分别是边
中,E、F分别是边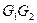 、
、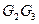 的中点,D是EF的中点,现沿SE、SF及EF把这个正方形折成一个几何体(如图乙所示),使
的中点,D是EF的中点,现沿SE、SF及EF把这个正方形折成一个几何体(如图乙所示),使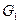 、
、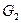 、
、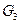 三点重合于点G,则下面结论成立的是( )
三点重合于点G,则下面结论成立的是( )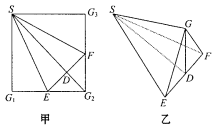
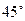 圈上有两点
圈上有两点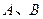 ,点
,点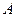 在东经
在东经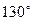 处,点
处,点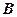 在西经
在西经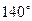 处,若地球半径为
处,若地球半径为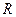 ,则
,则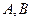 两点的球面距离为 _____________
两点的球面距离为 _____________