题目内容
已知等差数列{an}的前n项和为Sn,且a2=1,S11=33.
(1)求{an}的通项公式;
(2)设 ,求证:数列{bn}是等比数列,并求其前n项和Tn.
,求证:数列{bn}是等比数列,并求其前n项和Tn.
(1)求{an}的通项公式;
(2)设
 ,求证:数列{bn}是等比数列,并求其前n项和Tn.
,求证:数列{bn}是等比数列,并求其前n项和Tn.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:解题思路:(1)利用方程思想,用
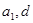 表示
表示 ,解得
,解得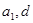 ,即得通项公式;(2)利用
,即得通项公式;(2)利用 证明等比数列,用等比数列求和公式进行求和.规律总结:等差数列、等比数列的已知量要注意利用方程思想,即
证明等比数列,用等比数列求和公式进行求和.规律总结:等差数列、等比数列的已知量要注意利用方程思想,即 的方程组.
的方程组.试题解析:(1)
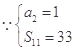 ,
, ,解得
,解得 ,
, ,
, ;
; (2)
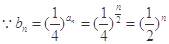 ,
, 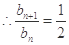 ,
,于是数列
 是以
是以 为首项,
为首项, 为公比的等比数列;
为公比的等比数列;其前
 项的和
项的和  .
. 
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
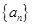 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项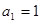 ,
,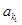 、
、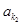 、 、
、 、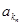 恰为等比数列,且
恰为等比数列,且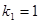 ,
,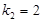 ,
,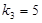 .
.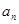 ;
;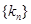 的前
的前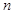 项和为
项和为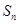 ,求
,求 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点 在曲线
在曲线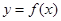 上
上 ,且
,且 .
.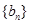 的前n项和为
的前n项和为 ,且满足
,且满足 ,问:当
,问:当 为何值时,数列
为何值时,数列 中,
中, ,对
,对 总有
总有 成立,
成立, 的值;
的值; ,并用数学归纳法证明
,并用数学归纳法证明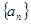 满足
满足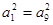 ,则数列
,则数列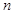 项和
项和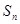 取最大值时,
取最大值时, 中,若
中,若 则
则
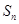 是等差数列
是等差数列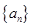 的前
的前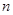 项和,若
项和,若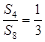 ,则
,则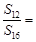 ( )
( )



 中,若
中,若 则
则 .
.