题目内容
已知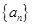 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项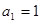 ,
,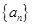 的部分项
的部分项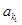 、
、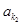 、 、
、 、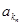 恰为等比数列,且
恰为等比数列,且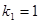 ,
,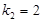 ,
,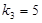 .
.
(1)求数列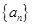 的通项公式
的通项公式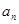 ;
;
(2)若数列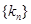 的前
的前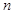 项和为
项和为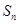 ,求
,求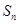 .
.
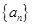 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项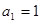 ,
,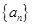 的部分项
的部分项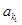 、
、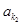 、 、
、 、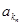 恰为等比数列,且
恰为等比数列,且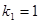 ,
,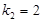 ,
,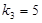 .
.(1)求数列
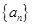 的通项公式
的通项公式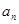 ;
;(2)若数列
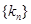 的前
的前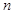 项和为
项和为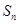 ,求
,求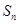 .
.(1) ;(2)
;(2)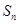
 .
.
 ;(2)
;(2)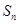
 .
.试题分析:(1)由于数列
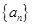 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项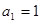 ,若设公差为d,则有
,若设公差为d,则有 ,又由已知可得
,又由已知可得 ,
, ,
, 成等比数列,所以
成等比数列,所以 ,然后将通项公式代入就可得到关于d的一个方程,再注意到
,然后将通项公式代入就可得到关于d的一个方程,再注意到 ,从而就可求出d的值,进而写出数列
,从而就可求出d的值,进而写出数列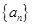 的通项公式
的通项公式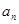 ;(2)由数列
;(2)由数列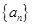 的部分项
的部分项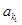 、
、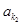 、……、
、……、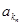 恰为等比数列,由(1)得到
恰为等比数列,由(1)得到 的通项公式,再由等比数列的概念得到公比
的通项公式,再由等比数列的概念得到公比 ,从而又可写出
,从而又可写出 的通项公式,这样两个
的通项公式,这样两个 的通项公式相同,就可求出数列
的通项公式相同,就可求出数列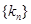 的通项公式,从而就可求出其前n项和
的通项公式,从而就可求出其前n项和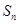 .
.试题解析:(1)
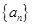 为公差不为
为公差不为 ,
,由已知得
 ,
, ,
, 成等比数列,
成等比数列,∴
 ,又
,又 1分
1分得
 2分
2分所以

 . 5分
. 5分(2)由(1)可知
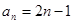 ∴
∴  7分
7分而等比数列
 的公比
的公比 ,
,
 9分
9分∴
 =
= ,
,∴
 即
即 
 11分
11分∴


 14分
14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求证:数列{bn}是等比数列,并求其前n项和Tn.
,求证:数列{bn}是等比数列,并求其前n项和Tn. a3,a2成等差数列,则
a3,a2成等差数列,则 =( ).
=( ).



 中,
中, ,
,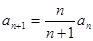 ,则
,则 中,若
中,若 ,则
,则 的值为( )
的值为( )
 的前
的前 项和为
项和为 ,若
,若 ,则
,则 ( )
( )

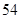

 }中,已知a
}中,已知a =2,a
=2,a +a
+a =13,则a
=13,则a 等于( )
等于( )