题目内容
已知 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点 在曲线
在曲线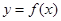 上
上 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列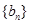 的前n项和为
的前n项和为 ,且满足
,且满足 ,问:当
,问:当 为何值时,数列
为何值时,数列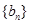 是等差数列.
是等差数列.
 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点 在曲线
在曲线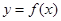 上
上 ,且
,且 .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
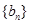 的前n项和为
的前n项和为 ,且满足
,且满足 ,问:当
,问:当 为何值时,数列
为何值时,数列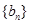 是等差数列.
是等差数列.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:解题思路:(1)根据条件寻找
 的递推关系,再求通项公式;(2)利用等差数列的前
的递推关系,再求通项公式;(2)利用等差数列的前 项和公式的特点(等差数列的前
项和公式的特点(等差数列的前 项和是关于
项和是关于 的一元二次函数,且常数项为0)求解.规律总结:根据数列的首项(或前几项)和递推公式求通项公式,要合理配凑,转化成等差数列或等比数列进行求解;判定数列是等差数列的方法一般有:①定义法;②中项法;③通项法;④前
的一元二次函数,且常数项为0)求解.规律总结:根据数列的首项(或前几项)和递推公式求通项公式,要合理配凑,转化成等差数列或等比数列进行求解;判定数列是等差数列的方法一般有:①定义法;②中项法;③通项法;④前 项和法.
项和法.试题解析:(1)由于
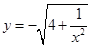 ,点
,点 在曲线
在曲线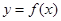 上,
上, ,并且
,并且 ,
, 。数列
。数列 是等差数列,首项
是等差数列,首项 ,公差d为4,
,公差d为4,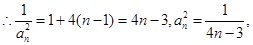

(2)由题意,得:
 故:
故: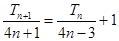 ,
, 为等差数列,其首项为
为等差数列,其首项为 ,公差为1.
,公差为1.
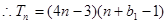
若要
 为等差数列,则
为等差数列,则 ,所以:
,所以: .
.
练习册系列答案
相关题目
 的前
的前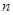 项和为
项和为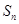 ,满足
,满足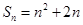 .等比数列
.等比数列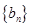 满足:
满足: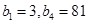 .
.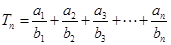 ,求
,求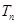 .
.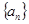 的首项
的首项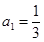 ,公比
,公比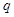 满足
满足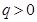 且
且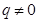 ,又已知
,又已知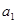 ,
,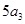 ,
,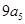 ,成等差数列;
,成等差数列;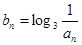 ,求
,求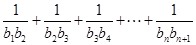 的值;
的值; ,求证:数列{bn}是等比数列,并求其前n项和Tn.
,求证:数列{bn}是等比数列,并求其前n项和Tn. 是首项
是首项 的递增等差数列,
的递增等差数列, 为其前
为其前 项和,且
项和,且 .
. 满足
满足 ,
, 为数列
为数列 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. a3,a2成等差数列,则
a3,a2成等差数列,则 =( ).
=( ).



 中,若
中,若 ,则
,则 的值为( )
的值为( )
 为等差数列
为等差数列 的前
的前 项和,
项和, ,
, ,则
,则 ( )
( )
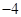


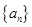 满足
满足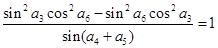 ,公差
,公差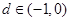 ,当且仅当
,当且仅当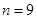 时,数列
时,数列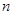 项和
项和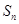 取得最大值,求该数列首项
取得最大值,求该数列首项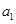 的取值范围
的取值范围


