题目内容
数列{an}的前n项和Sn=n2-4n+2,则|a1|+|a2|+…+|a10|=________.
66
当n=1时,a1=S1=-1.
当n≥2时,an=Sn-Sn-1=2n-5.
∴
令2n-5≤0,得n≤ ,
,
∴当n≤2时,an<0,当n≥3时,an>0,
∴|a1|+|a2|+…+|a10|=-(a1+a2)+(a3+a4+…+a10)=S10-2S2=66.
当n≥2时,an=Sn-Sn-1=2n-5.
∴

令2n-5≤0,得n≤
 ,
,∴当n≤2时,an<0,当n≥3时,an>0,
∴|a1|+|a2|+…+|a10|=-(a1+a2)+(a3+a4+…+a10)=S10-2S2=66.

练习册系列答案
相关题目
 ,求证:数列{bn}是等比数列,并求其前n项和Tn.
,求证:数列{bn}是等比数列,并求其前n项和Tn. 是首项
是首项 的递增等差数列,
的递增等差数列, 为其前
为其前 项和,且
项和,且 .
. 满足
满足 ,
, 为数列
为数列 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的前
的前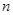 项和为
项和为 ,
, ,
, ,
, ,求数列
,求数列 的前100项和.
的前100项和. 的前n项和
的前n项和 ,(1)求实数
,(1)求实数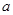 的值;(2)求数列
的值;(2)求数列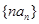 的前n项和
的前n项和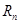 .
. 满足
满足 .
. ;
; 的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分)
的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分) (ab)= a
(ab)= a (n∈N*), bn=
(n∈N*), bn= (n∈N*).
(n∈N*). 是等差数列,其中
是等差数列,其中 ,前四项和
,前四项和 .
. ,①求数列
,①求数列 的前
的前 项之和
项之和
 是不是数列
是不是数列 满足
满足
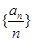 是等差数列;
是等差数列;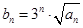 ,求数列
,求数列 的前
的前 项和
项和