题目内容
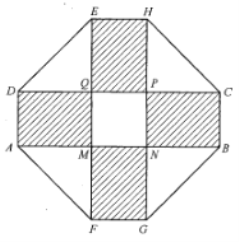
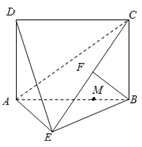
【题目】在如图所示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为边长为2的菱形,
为边长为2的菱形, ![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
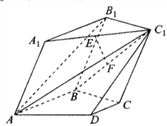
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)第(1)问,转化成证明![]() 平面
平面![]() ,再转化成证明
,再转化成证明![]() 和
和![]() .(2)第(2)问,先利用几何法找到
.(2)第(2)问,先利用几何法找到![]() 与平面
与平面![]() 所成角,再根据
所成角,再根据![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 求出
求出![]() 再建立空间直角坐标系,求出二面角
再建立空间直角坐标系,求出二面角![]() 的余弦值.
的余弦值.
试题解析:
(1)连接![]() ,因为四边形
,因为四边形![]() 为菱形,所以
为菱形,所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 分别为
分别为![]() ,
, ![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() 平面
平面![]()
(2)设![]() ,由(1)得
,由(1)得![]() 平面
平面![]() .
.
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() .
.
过点![]() 作
作![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,如图所示,
,如图所示,
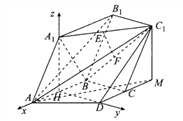
又![]() ,所以
,所以![]() 为等边三角形,所以
为等边三角形,所以![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
因为![]() 为平行四边形,所以
为平行四边形,所以![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
由(1),得![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 是
是![]() 与平面
与平面![]() 所成角.
所成角.
因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,因为
,因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
所以![]() ,
, 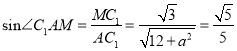 ,解得
,解得![]() .
.
在梯形![]() 中,易证
中,易证![]() ,分别以
,分别以![]() ,
, ![]() ,
, ![]() 的正方向为
的正方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系.
轴的正方向建立空间直角坐标系.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
由![]() ,及
,及![]() ,得
,得![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由![]() 得
得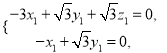 令
令![]() ,得m=(3,1,2)
,得m=(3,1,2)
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由 得
得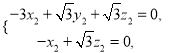 令
令![]() ,得
,得![]() .
.
所以![]()
又因为二面角![]() 是钝角,所以二面角
是钝角,所以二面角![]() 的余弦值是
的余弦值是![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在甲、乙两个班级进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下的2×2列联表.已知在全部105人中抽到随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可能性要求,能否认为“成绩与班级有关系”?
P(K2≥x0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式及数据:K2=![]() .
.