题目内容
【题目】已知椭圆C:![]() 1(a>b>0)的左右焦点分别为F1,F2,点P是椭圆C上一点,以PF1为直径的圆E:x2
1(a>b>0)的左右焦点分别为F1,F2,点P是椭圆C上一点,以PF1为直径的圆E:x2 过点F2.
过点F2.
(1)求椭圆C的方程;
(2)过点P且斜率大于0的直线l1与C的另一个交点为A,与直线x=4的交点为B,过点(3,![]() )且与l1垂直的直线l2与直线x=4交于点D,求△ABD面积的最小值.
)且与l1垂直的直线l2与直线x=4交于点D,求△ABD面积的最小值.
【答案】(1)![]() ;(2)2
;(2)2![]() 2
2![]() .
.
【解析】
(1)根据题意求得椭圆的焦点坐标,利用椭圆的定义求得a和b的值,即可求得椭圆方程;
(2)设直线l1的方程,代入涂鸦方程,利用韦达定理求得A的横坐标,求得直线l2方程,求得D点坐标,利用三角形的面积公式及基本不等式即可求得△ABD面积的最小值.
(1)在圆E的方程中,令y=0,得到:x2=4,
所以F1(﹣2,0),F2(2,0),
又因为![]() ,所以P点坐标为
,所以P点坐标为![]() ,
,
所以![]() ,则
,则![]() ,b=2,
,b=2,
因此椭圆的方程为![]() ;
;
(2)设直线l1:y![]() k(x﹣2)(k>0),
k(x﹣2)(k>0),
所以点B的坐标为![]() ,
,
设A(xA,yA),D(xD,yD),将直线l1代入椭圆方程得:(1+2k2)x2+(4![]() k﹣8k2)x+8k2﹣8
k﹣8k2)x+8k2﹣8![]() k﹣4=0,
k﹣4=0,
所以xPxA![]() ,所以xA
,所以xA![]() ,
,
直线l2的方程为y![]() (x﹣3),所以点D坐标为
(x﹣3),所以点D坐标为![]() ,
,
所以S△ABD![]() (4﹣xA)|yB﹣yD|
(4﹣xA)|yB﹣yD|![]()
![]()
![]()
=2k![]() 2
2![]() 2
2![]() 2
2![]() ,
,
当且仅当2k![]() ,即k
,即k![]() 时取等号,
时取等号,
综上,△ABD面积的最小值2![]() 2
2![]() .
.

【题目】某大学高等数学这学期分别用![]() 两种不同的数学方式试验甲、乙两个大一新班(人数均为
两种不同的数学方式试验甲、乙两个大一新班(人数均为![]() 人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各
人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各![]() 名的高等数学期末考试成绩,得到茎叶图:
名的高等数学期末考试成绩,得到茎叶图:


(1)学校规定:成绩不得低于85分的为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
下面临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考方式:![]() ,其中
,其中![]() )
)
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
【题目】2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为( )
A.20B.30C.35D.40
【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.
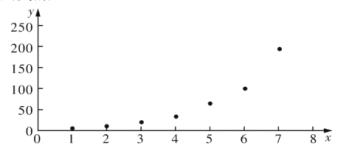
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次.
的回归方程,并预测活动推出第8天使用扫码支付的人次.
(3)推广期结束后,为更好的服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
人次 | 10 | 60 | 30 |
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调査结果发现:使用扫码支付的乘客中有5名乘客享受7折优惠,有10名乘客享受8折优惠,有15名乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: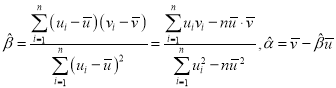 .
.




