题目内容
6.在极坐标中,若实数ρ,θ满足3ρcos2θ+2ρsin2θ=6cosθ,则ρ2的最大值为4.分析 实数ρ,θ满足3ρcos2θ+2ρsin2θ=6cosθ,化为$ρ=\frac{6cosθ}{co{s}^{2}θ+2}$,由于ρ是偶函数,只考虑cosθ>0时,变形ρ=$\frac{6}{cosθ+\frac{2}{cosθ}}$,通过换元求导研究其单调性即可得出.
解答 解:实数ρ,θ满足3ρcos2θ+2ρsin2θ=6cosθ,
化为$ρ=\frac{6cosθ}{co{s}^{2}θ+2}$,
由于ρ是偶函数,只考虑cosθ>0时,
ρ=$\frac{6}{cosθ+\frac{2}{cosθ}}$,
设m=$cosθ+\frac{2}{cosθ}$,令cosθ=t∈(0,1],
∴$m=t+\frac{2}{t}$,m′=1-$\frac{2}{{t}^{2}}$=$\frac{{t}^{2}-2}{{t}^{2}}$<0,
因此函数m(t)单调递减,当t=1时,函数m(t)取得最小值3,此时ρ取得最大值2,因此ρ2取得最大值4.
故答案为:4.
点评 本题考查了极坐标方程的应用、三角函数的单调性、换元法、利用导数研究函数单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.根据如下样本数据
得到的回归方程为$\hat y=bx+a$,则( )
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | -4.0 | -2.5 | 0.5 | -0.5 | 2.0 | 3.0 |
| A. | a>0,b<0 | B. | a>0,b>0 | C. | a<0,b<0 | D. | a<0,b>0 |
11.已知l1⊥l2,直线l1的倾斜角为45°,则直线l2的倾斜角为( )
| A. | 45° | B. | 135° | C. | -45° | D. | 120° |
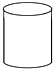
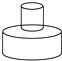
 用均匀的速度向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OAB为一折线),这个容器的形状是图中( )?
用均匀的速度向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OAB为一折线),这个容器的形状是图中( )?