题目内容
5.公园中有一个月亮门,上边是半径为$\frac{\sqrt{17}}{2}$m的圆的劣弧,下边是长半轴等于2m,短半轴等于1m的半个椭圆,现要搬运一个横截面为矩形的货箱水平通过该月亮门.若矩形货箱的横截面的水平底边长为2m,则该货箱的高所允许的最大值为多少m.分析 通过建立平面直角坐标系,可得EF即为所求最大值,利用勾股定理及两点间的距离公式计算即可.
解答 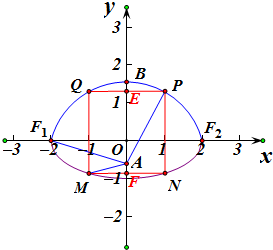 解:建立平面直角坐标系如图,椭圆方程为$\frac{{x}^{2}}{4}$+y2=1,
解:建立平面直角坐标系如图,椭圆方程为$\frac{{x}^{2}}{4}$+y2=1,
设A为劣弧所在圆的圆心,则OA=$\sqrt{A{{F}_{1}}^{2}-O{F}^{2}}$=$\sqrt{\frac{17}{4}-4}$=$\frac{1}{2}$,即A(0,-$\frac{1}{2}$),
设货箱的横截面为MNPQ,则MN=PQ=2,
则EF即为所求最大值,
此时M(-1,-$\frac{\sqrt{3}}{2}$),∴F(0,-$\frac{\sqrt{3}}{2}$),
∴AF=$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$,
在Rt△AEP中,AE=$\sqrt{A{P}^{2}-E{P}^{2}}$=$\sqrt{\frac{17}{4}-1}$=$\frac{\sqrt{13}}{2}$,
∴EF=AE+AF=$\frac{\sqrt{13}}{2}$+$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$,
故该货箱的高所允许的最大值为$\frac{\sqrt{13}}{2}$+$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$m.
点评 本题是一道关于椭圆与圆的应用题,建系画出图形、找出最大值时的情形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
10.若x,y∈R,则“log2(xy+4x-2y)=3”是“x2-4x+y2+8y+20=0”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.设全集U=R,已知A={x|$\frac{2x+3}{x-2}$>0},B={x||x-1|<2},则(∁UA)∩B=( )
| A. | (-$\frac{3}{2}$,-1) | B. | (-1,-2] | C. | (2,3] | D. | [2,3) |
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+$\frac{1}{2}$∠A; ②EF=BE+CF;③设OD=m,AE+AF=n,则S△AEF=$\frac{1}{2}$mn; ④EF是△ABC的中位线.其中正确的结论是①②③.
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+$\frac{1}{2}$∠A; ②EF=BE+CF;③设OD=m,AE+AF=n,则S△AEF=$\frac{1}{2}$mn; ④EF是△ABC的中位线.其中正确的结论是①②③. 在△ABC中,已知CM是∠ACB的平分线,△AMC的外接圆交BC于点N.若2AB=AC,AM=$\sqrt{2}$,求BN的长.
在△ABC中,已知CM是∠ACB的平分线,△AMC的外接圆交BC于点N.若2AB=AC,AM=$\sqrt{2}$,求BN的长. 如图:钝角三角形ABC的面积为18,最长边AB=12,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为3.
如图:钝角三角形ABC的面积为18,最长边AB=12,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为3.