题目内容
11.已知l1⊥l2,直线l1的倾斜角为45°,则直线l2的倾斜角为( )| A. | 45° | B. | 135° | C. | -45° | D. | 120° |
分析 由题意,两条直线的斜率都存在,直线垂直则斜率互为负倒数,由此得到直线l2的斜率,求倾斜角.
解答 解:因为l1⊥l2,直线l1的倾斜角为45°,所以直线l1的斜率为tan45°=1,
所以${k}_{{l}_{1}}•{k}_{{l}_{2}}=-1$,所以直线l2的斜率为-1,
所以其倾斜角为135°;
故选B.
点评 本题考查了直线垂直与直线倾斜角的关系;关键是得到斜率的关系.直线垂直,如果斜率都存在,则向量互为负倒数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若集合A={x|-x2+7x-10<0}与B={x||2x+1|<3},则下列选项中正确的是( )
| A. | A⊆B | B. | A?B | C. | B?A | D. | A=B |
10.若x,y∈R,则“log2(xy+4x-2y)=3”是“x2-4x+y2+8y+20=0”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
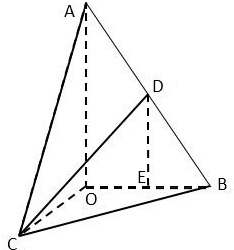 如图,已知正三角形ABC的边长为6,将△ABC沿BC边上的高线AO折起,使BC=3$\sqrt{2}$,得到三棱锥A-BOC.动点D在边AB上.
如图,已知正三角形ABC的边长为6,将△ABC沿BC边上的高线AO折起,使BC=3$\sqrt{2}$,得到三棱锥A-BOC.动点D在边AB上.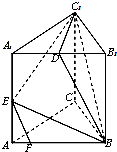 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.