题目内容
(本题满分14分)如图,在长方体ABCD—A1B1C1D1中,AB= AD=2.
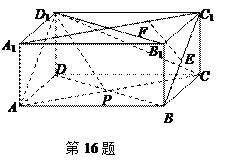
(1)证明:面BDD1 B1⊥面ACD1;
(2)若E是BC1的中点,P是AC的中点,F是A1C1上的点, C1F=mFA1,试求m的值,使得EF∥D1P.
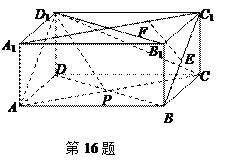
(1)证明:面BDD1 B1⊥面ACD1;
(2)若E是BC1的中点,P是AC的中点,F是A1C1上的点, C1F=mFA1,试求m的值,使得EF∥D1P.
(1)略(2)略
证明(1):在长方体ABCD—A1B1C1D1中,AB= AD=2,故四边形ABCD是正方形,AP⊥DP,又∵D1D⊥面ABCD,AP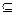 面ABCD∴D1D⊥AP ,D1D∩DP=D∴AP⊥面BDD1B1 ∵AP
面ABCD∴D1D⊥AP ,D1D∩DP=D∴AP⊥面BDD1B1 ∵AP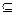 面AD1C
面AD1C
∴面BDB1D1⊥面ACD1 ----7分
解(2):记A1C1与B1D1的交点为Q,连BQ,
∵P是AC的中点,∴D1P∥BQ,要使得EF∥D1P,则必有EF∥BQ
在△QBC1中,E是BC1的中点, F是QC1上的点,EF∥BQ
∴F是QC1的中点,即3C1F=FA1,故所求m的值是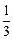 . ----14分
. ----14分
点评:本题考查空间想象能力、逻辑推理能力,线面平行、线面垂直、面面平行、面面垂直,属于中档题,
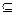 面ABCD∴D1D⊥AP ,D1D∩DP=D∴AP⊥面BDD1B1 ∵AP
面ABCD∴D1D⊥AP ,D1D∩DP=D∴AP⊥面BDD1B1 ∵AP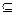 面AD1C
面AD1C∴面BDB1D1⊥面ACD1 ----7分
解(2):记A1C1与B1D1的交点为Q,连BQ,
∵P是AC的中点,∴D1P∥BQ,要使得EF∥D1P,则必有EF∥BQ
在△QBC1中,E是BC1的中点, F是QC1上的点,EF∥BQ
∴F是QC1的中点,即3C1F=FA1,故所求m的值是
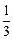 . ----14分
. ----14分点评:本题考查空间想象能力、逻辑推理能力,线面平行、线面垂直、面面平行、面面垂直,属于中档题,

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
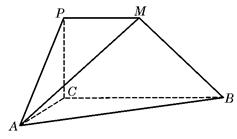 如图,
如图, 是直角梯形,∠
是直角梯形,∠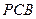 =90°,
=90°,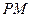 ∥
∥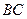 ,
,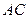 =1,∠
=1,∠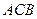 =120°,
=120°,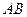 ⊥
⊥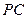 ,直线
,直线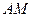 与直线
与直线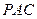 ⊥平面
⊥平面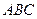 ;
;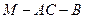 的大小;
的大小;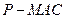 的体积.
的体积.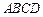 中,
中,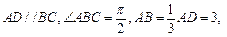

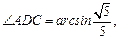
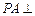 平面
平面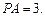
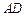 与
与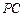 间的距离;
间的距离;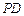 与平面
与平面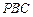 所成的角;
所成的角;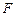 是线段
是线段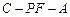 的
的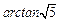 ,求AF.
,求AF.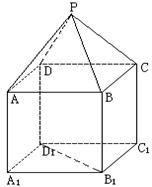
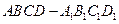 是正方体,其中
是正方体,其中

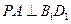 ;
;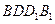 所成角
所成角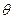 的余弦值;
的余弦值;








 (2)平面AB1D与侧面BB1C1C所成锐角的大小 C1 B1
(2)平面AB1D与侧面BB1C1C所成锐角的大小 C1 B1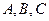 三点,
三点,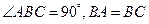 ,球心
,球心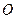 到平面
到平面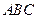 的距离是
的距离是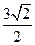 ,则
,则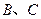 两点的球面距离是( )
两点的球面距离是( )