题目内容
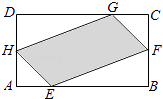
【题目】如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2. 
(1)求证:AF∥平面CDE;
(2)求平面AEF与平面ABCD所成锐二面角的余弦值.
【答案】
(1)证明:以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴,
建立如图所示空间直角坐标系.
则C(0,0,0),B(2,0,0),D(0,0,4),E(0,4,0),A(2,0,4),F(2,2,0),
则 ![]() =(0,2,﹣4),
=(0,2,﹣4), ![]() =(2,0,0).
=(2,0,0).
![]() =(2,0,0)为平面CDE的一个法向量.
=(2,0,0)为平面CDE的一个法向量.
又 ![]() =0,AF平面CDE,
=0,AF平面CDE,
∴AF∥平面CDE.
(2)解:设平面AEF的一个法向量为 ![]() =(x1,y1,z1),则
=(x1,y1,z1),则  ,
,
∵ ![]() ,
,
∴ ![]() ,取z1=1,得
,取z1=1,得 ![]() .
.
又∵CE⊥平面ABCD,∴平面ABCD一个法向量为 ![]() ,
,
设平面ADE与平面BCEF所成锐二面角的大小为α,
则 
因此,平面ADE与平面BCEF所成锐二面角的余弦值为 ![]() .
.

【解析】(1)以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴,建立空间直角坐标系.利用向量法能证明AF∥平面CDE.(2)求出平面AEF的一个法向量和平面ABCD一个法向量,利用向量法能求出平面ADE与平面BCEF所成锐二面角的余弦值.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目