Question

【题目】如图，设圆弧x2+y2=1（x≥0，y≥0）与两坐标轴正半轴围成的扇形区域为M，过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N．现随机在区域N内投一点B，若设点B落在区域M内的概率为P，则P的值为（　　）

A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：∵A是圆弧上的中点，
∴A（1，1），
则OA的斜率为k=1，
则过A的直线方程为y﹣1=﹣（x﹣1），即y=﹣x+2，
则直线y=﹣x+2与坐标轴的交点为（2，0），（0，2）对应三角形的面积S=x2x2=2，
M的面积S=
则点B落在区域M内的概率为P=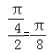
故选：B
【考点精析】本题主要考查了几何概型的相关知识点，需要掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能正确解答此题．