题目内容
当a,b,c∈(0,+∞)时,由 ≥
≥ ,
, ≥
≥ ,运用归纳推理,可猜测出的合理结论是( )
,运用归纳推理,可猜测出的合理结论是( )
A. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
B. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
C. ≥ ≥ (ai∈R,i=1,2,…n) (ai∈R,i=1,2,…n) |
D. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
D
解析试题分析:根据题意,由于a,b,c∈(0,+∞)时,由 ≥
≥ ,
, ≥
≥ ,那么可知左边是n个数的算术平均值,右边是几何平均值,那么可知得到
,那么可知左边是n个数的算术平均值,右边是几何平均值,那么可知得到 ≥
≥ (ai>0,i=1,2,…n)成立故选D.
(ai>0,i=1,2,…n)成立故选D.
考点:归纳推理
点评:主要是考查了归纳推理的运用,属于基础题。

练习册系列答案
相关题目
设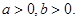 若
若 的最小值为( )
的最小值为( )
| A.8 | B.4 | C.1 | D.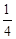 |
设 的最小值是( )
的最小值是( )
| A.10( | B. | C. | D. |
设x>0,y>0,x+y+xy=2,则x+y的最小值是( )
A.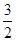 | B.1 + 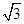 | C.2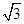 -2 -2 | D.2-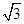 |
设 ,则
,则 三数中( )
三数中( )
| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
点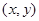 在直线
在直线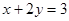 上移动,则
上移动,则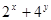 的最小值为( )
的最小值为( )
A.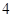 | B.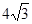 | C. | D. |
如果 ,那么
,那么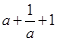 的最小值是( )
的最小值是( )
| A.2 | B.3 | C.4 | D.5 |
已知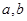 是不相等的正数,且
是不相等的正数,且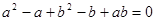 ,则
,则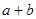 的取值范围是
的取值范围是
A.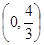 | B.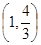 | C. | D.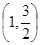 |
对于使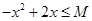 成立的所有常数
成立的所有常数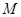 中,我们把
中,我们把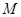 的最小值
的最小值 叫做
叫做 的上确界,若
的上确界,若 ,则
,则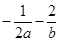 的上确界为 ( )
的上确界为 ( )
| A.-3 | B. | C.- | D. |