题目内容
已知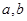 是不相等的正数,且
是不相等的正数,且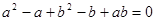 ,则
,则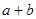 的取值范围是
的取值范围是
A.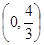 | B.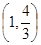 | C. | D.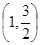 |
B
解析试题分析: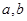 是不相等的正数,且
是不相等的正数,且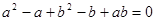 ,由于
,由于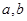 是不相等的正数,且
是不相等的正数,且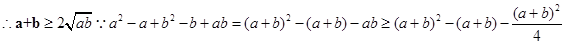 即可知
即可知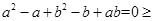
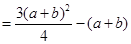 ,解二次不等式可知,
,解二次不等式可知,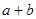 取值范围
取值范围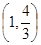 ,选B.
,选B.
考点:均值不等式
点评:解决关键是根据不等式的性质,结合重要不等式,进行求解范围,属于基础题。

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
当a,b,c∈(0,+∞)时,由 ≥
≥ ,
, ≥
≥ ,运用归纳推理,可猜测出的合理结论是( )
,运用归纳推理,可猜测出的合理结论是( )
A. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
B. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
C. ≥ ≥ (ai∈R,i=1,2,…n) (ai∈R,i=1,2,…n) |
D. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
下列各式中,最小值等于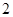 的是( )
的是( )
A.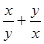 | B.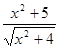 | C.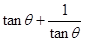 | D.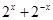 |
已知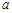 ,
,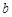 为实数,且
为实数,且 ,则下列命题错误的是
,则下列命题错误的是
A.若 , , ,则 ,则 | B.若 ,则 ,则 , , |
C.若 ,则 ,则 | D.若 ,则 ,则 |
设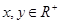 且
且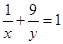 ,则
,则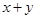 的最小值为( )
的最小值为( )
| A.12 | B.15 | C.16 | D.-16 |
设 是实数,且满足等式
是实数,且满足等式 ,则实数
,则实数 等于( )(以下各式中
等于( )(以下各式中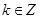 )
)
A.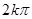 | B. | C. | D. |
.已知实数 ,则M的最小值为( )
,则M的最小值为( )
A. | B.2 | C.4 | D.1 |
设 若3是
若3是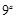 与
与 的等比中项,则
的等比中项,则 的最小值为
的最小值为
| A.12 | B.24 | C.25 | D.36 |
 是
是 内一点,且
内一点,且 的面积为2,定义
的面积为2,定义 ,其中
,其中 分别是ΔMBC,ΔMCA,ΔMAB的面积,若
分别是ΔMBC,ΔMCA,ΔMAB的面积,若 满足
满足 ,则
,则 的最小值是( )
的最小值是( )