题目内容
对于使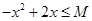 成立的所有常数
成立的所有常数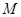 中,我们把
中,我们把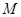 的最小值
的最小值 叫做
叫做 的上确界,若
的上确界,若 ,则
,则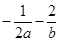 的上确界为 ( )
的上确界为 ( )
| A.-3 | B. | C.- | D. |
D
解析试题分析:由题意知相当于求 的最大值,将a+b=1代入,
的最大值,将a+b=1代入,
又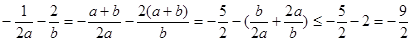 ,故选(
,故选( )
)
考点:本题主要考查了均值不等式的求解最值的问题的运用。
点评:解决该试题的关键是构造均值不等式的结构特点来求解最值。注意整体的思想,先通分合并,然后将a+b=1,整体代入得到。

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
当a,b,c∈(0,+∞)时,由 ≥
≥ ,
, ≥
≥ ,运用归纳推理,可猜测出的合理结论是( )
,运用归纳推理,可猜测出的合理结论是( )
A. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
B. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
C. ≥ ≥ (ai∈R,i=1,2,…n) (ai∈R,i=1,2,…n) |
D. ≥ ≥ (ai>0,i=1,2,…n) (ai>0,i=1,2,…n) |
设 是实数,且满足等式
是实数,且满足等式 ,则实数
,则实数 等于( )(以下各式中
等于( )(以下各式中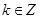 )
)
A.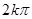 | B. | C. | D. |
.已知实数 ,则M的最小值为( )
,则M的最小值为( )
A. | B.2 | C.4 | D.1 |
已知x,y 都是正数,若  , 则
, 则 有( )
有( )
| A.最小值16 | B.最大值16 | C.最小值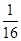 | D.最大值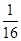 |
正实数 满足
满足 设
设 ,则:
,则:
| A.p>2012 | B.p=2012 | C.p<2012 | D.p≤2012 |
已知 ,函数
,函数 的最小值是 ( )
的最小值是 ( )
| A.5 | B.4 | C.8 | D.6 |
设 若3是
若3是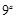 与
与 的等比中项,则
的等比中项,则 的最小值为
的最小值为
| A.12 | B.24 | C.25 | D.36 |
 +
+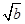 ≤
≤ ;③a2+b2≥2;④a3+b3≥3;⑤
;③a2+b2≥2;④a3+b3≥3;⑤ +
+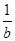 ≥2.
≥2.