题目内容
已知椭圆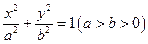 的离心率
的离心率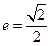 ,短轴长为
,短轴长为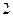 .
.
(Ⅰ)求椭圆方程;(Ⅱ)若椭圆与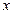 轴正半轴、
轴正半轴、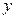 轴正半轴的交点分别为
轴正半轴的交点分别为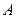 、
、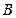 ,经过点
,经过点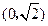 且斜率为
且斜率为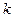 的直线
的直线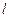 与椭圆交于不同的两点
与椭圆交于不同的两点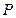 、
、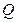 .是否存在常数
.是否存在常数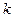 ,使得向量
,使得向量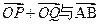 共线?如果存在,求
共线?如果存在,求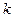 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
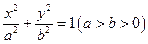 的离心率
的离心率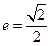 ,短轴长为
,短轴长为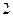 .
.(Ⅰ)求椭圆方程;(Ⅱ)若椭圆与
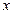 轴正半轴、
轴正半轴、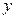 轴正半轴的交点分别为
轴正半轴的交点分别为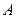 、
、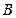 ,经过点
,经过点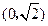 且斜率为
且斜率为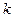 的直线
的直线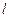 与椭圆交于不同的两点
与椭圆交于不同的两点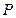 、
、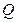 .是否存在常数
.是否存在常数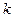 ,使得向量
,使得向量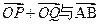 共线?如果存在,求
共线?如果存在,求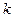 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.(Ⅰ)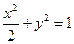 。(Ⅱ)不存在符合题意的常数
。(Ⅱ)不存在符合题意的常数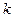 ,理由略。
,理由略。
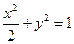 。(Ⅱ)不存在符合题意的常数
。(Ⅱ)不存在符合题意的常数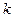 ,理由略。
,理由略。(1)椭圆方程是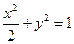 ……4分
……4分
(Ⅱ)由已知条件,直线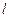 :
: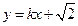 ,代入椭圆方程得
,代入椭圆方程得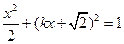 .
.
整理得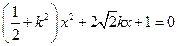 ①
①
由已知得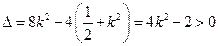 ,解得
,解得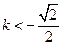 或
或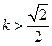 ……6分
……6分
设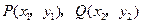 ,则
,则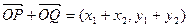 ,
,
由方程①,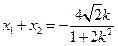 . ②
. ②
又 . ③
. ③
而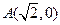 ,
,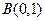 ,
,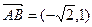 ,
,
所以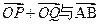 共线等价于
共线等价于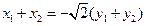 ,
,
将②③代入上式,解得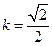 ,……10分
,……10分
又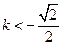 或
或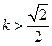 ,故没有符合题意的常数
,故没有符合题意的常数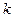 .………………12分
.………………12分
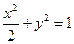 ……4分
……4分(Ⅱ)由已知条件,直线
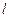 :
: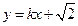 ,代入椭圆方程得
,代入椭圆方程得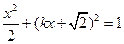 .
.整理得
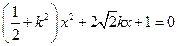 ①
①由已知得
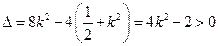 ,解得
,解得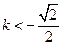 或
或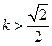 ……6分
……6分设
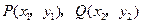 ,则
,则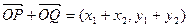 ,
,由方程①,
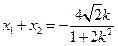 . ②
. ②又
 . ③
. ③而
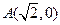 ,
,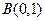 ,
,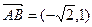 ,
,所以
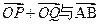 共线等价于
共线等价于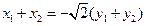 ,
,将②③代入上式,解得
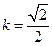 ,……10分
,……10分又
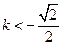 或
或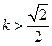 ,故没有符合题意的常数
,故没有符合题意的常数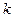 .………………12分
.………………12分
练习册系列答案
相关题目
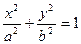 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P 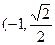 )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。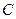 是椭圆上异于长轴端点的任一点,对于△ABC,求
是椭圆上异于长轴端点的任一点,对于△ABC,求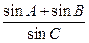 的值。
的值。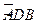 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.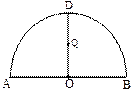
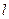 使
使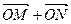 与
与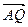 平行,若平行,求出直线
平行,若平行,求出直线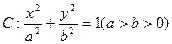 的离心率,
的离心率,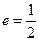 右焦点到直线
右焦点到直线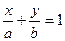 的距离
的距离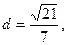
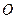 为坐标原点.
为坐标原点.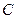 的方程;
的方程;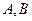 两点,证明:点
两点,证明:点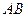 的距离为定值,并求弦
的距离为定值,并求弦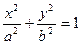
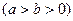 的离心率为
的离心率为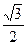 ,则双曲
,则双曲 的离心率为( )
的离心率为( )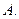

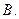
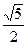
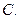
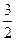
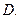
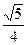
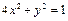 及直线
及直线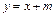 ,当直线被椭圆截得的弦最长时的直线方程为
,当直线被椭圆截得的弦最长时的直线方程为
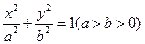 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量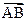 与
与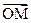 是共线向量
是共线向量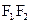 分别是左右焦点,求
分别是左右焦点,求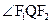 的取值范围
的取值范围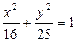 ,则此椭圆的离心率为
,则此椭圆的离心率为 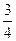
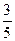
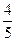
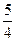
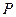 为椭圆
为椭圆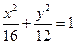 上任一点,当
上任一点,当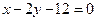 的距离的最小时,点
的距离的最小时,点