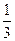题目内容
(本小题满分12分)
设椭圆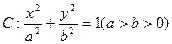 的离心率,
的离心率,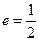 右焦点到直线
右焦点到直线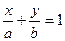 的距离
的距离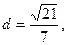
 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆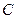 的方程;
的方程;
(II)过点 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆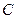 分别交于
分别交于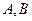 两点,证明:点
两点,证明:点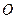 到直线
到直线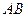 的距离为定值,并求弦
的距离为定值,并求弦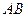 长度的最小值.
长度的最小值.
设椭圆
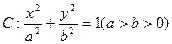 的离心率,
的离心率,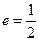 右焦点到直线
右焦点到直线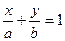 的距离
的距离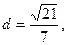
 为坐标原点.
为坐标原点.(Ⅰ)求椭圆
 的方程;
的方程;(II)过点
 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆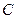 分别交于
分别交于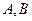 两点,证明:点
两点,证明:点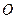 到直线
到直线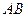 的距离为定值,并求弦
的距离为定值,并求弦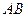 长度的最小值.
长度的最小值.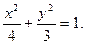 O到直线AB的距离
O到直线AB的距离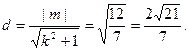 ,
, 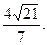
(I)由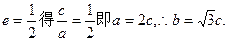
由右焦点到直线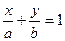 的距离为
的距离为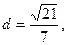
得: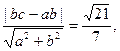 解得
解得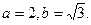
所以椭圆C的方程为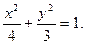 …………4分
…………4分
(II)设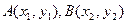 ,
,
直线AB的方程为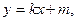
与椭圆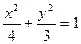 联立消去y得
联立消去y得
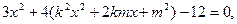
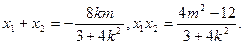
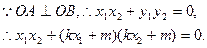
即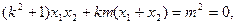
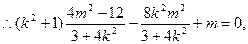
整理得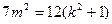 所以O到直线AB的距离
所以O到直线AB的距离
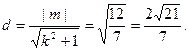 …………8分
…………8分
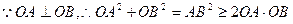 ,
,
当且仅当OA=OB时取“=”号。
由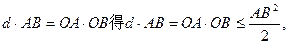
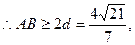
即弦AB的长度的最小值是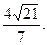 …………13分
…………13分
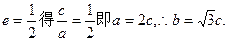
由右焦点到直线
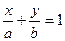 的距离为
的距离为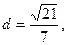
得:
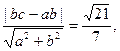 解得
解得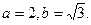
所以椭圆C的方程为
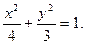 …………4分
…………4分(II)设
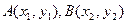 ,
,直线AB的方程为
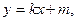
与椭圆
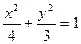 联立消去y得
联立消去y得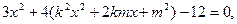
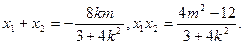
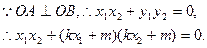
即
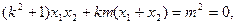
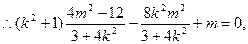
整理得
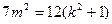 所以O到直线AB的距离
所以O到直线AB的距离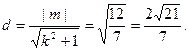 …………8分
…………8分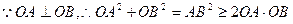 ,
, 当且仅当OA=OB时取“=”号。
由
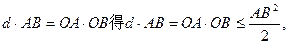
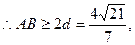
即弦AB的长度的最小值是
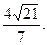 …………13分
…………13分
练习册系列答案
相关题目
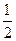 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;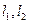 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,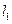 交E于A,B两点,
交E于A,B两点,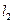 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。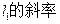 k的取值范围;
k的取值范围;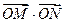 的取值范围。
的取值范围。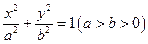 的离心率
的离心率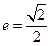 ,短轴长为
,短轴长为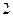 .
.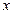 轴正半轴、
轴正半轴、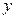 轴正半轴的交点分别为
轴正半轴的交点分别为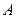 、
、 ,经过点
,经过点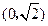 且斜率为
且斜率为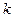 的直线
的直线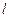 与椭圆交于不同的两点
与椭圆交于不同的两点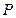 、
、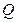 .是否存在常数
.是否存在常数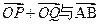 共线?如果存在,求
共线?如果存在,求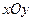 中有两定点
中有两定点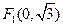 ,
,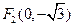 ,若动点M满足
,若动点M满足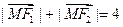 ,设动点M的轨迹为C。
,设动点M的轨迹为C。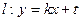 交曲线C于A、B两点,交直线
交曲线C于A、B两点,交直线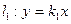 于点D,若
于点D,若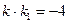 ,证明:D为AB的中点。
,证明:D为AB的中点。 2为椭圆
2为椭圆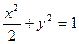 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线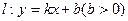 与圆O相切并与椭圆交于不同的两点A,B。
与圆O相切并与椭圆交于不同的两点A,B。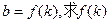 的表达式;
的表达式;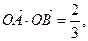 求直线
求直线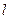 的方程;
的方程;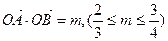 ,求三角形OAB面积的取值范围。
,求三角形OAB面积的取值范围。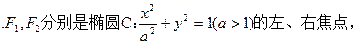 直线
直线 与C相交于A,B两点
与C相交于A,B两点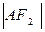 ,
,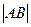 ,
,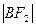 成等差数列,直线
成等差数列,直线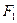 ,求a值
,求a值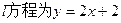 ,且
,且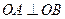 ,求a值
,求a值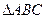 中顶点
中顶点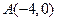 和顶点
和顶点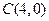 ,顶点
,顶点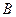 在椭圆
在椭圆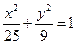 上,则
上,则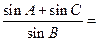
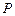 是椭圆
是椭圆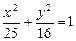 上一动点,
上一动点,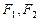 是椭圆的两个焦点,
是椭圆的两个焦点,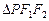 的内切圆半径为
的内切圆半径为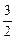 ,则当点点
,则当点点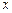 轴上方时,点
轴上方时,点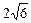

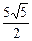
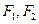 是椭圆的两个焦点,过
是椭圆的两个焦点,过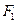 且与椭圆长轴垂直的弦交椭圆与
且与椭圆长轴垂直的弦交椭圆与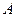 ,
,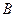 两点,
两点,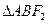 是正三角形,则椭圆的离心率是( )
是正三角形,则椭圆的离心率是( )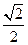 B
B 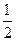 C
C 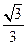 D
D