题目内容
17.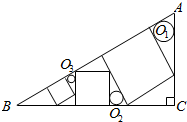 △ABC中,∠C=90°,作三个正方形及三个圆O1,O2,O3,如图,半径分别为r1,r2,r3.证明:r1r3=r${\;}_{2}^{2}$.
△ABC中,∠C=90°,作三个正方形及三个圆O1,O2,O3,如图,半径分别为r1,r2,r3.证明:r1r3=r${\;}_{2}^{2}$.
分析 证明三个正方形的边长为等比数列,所以其内接圆半径也是等比数列即可.
解答 证明:设ABC的三边为a,b,c,第一个正方形,将AC(b)边分成两段,分别属于两个与ABC相似的三角形
设正方形边长为x,则有x=(b-$\frac{b}{c}$x)•$\frac{a}{c}$,解得x=$\frac{abc}{{c}^{2}+ab}$,即边为a,b,c的直角三角形的内接正方形的边长
设第二个正方形边长为y,内接于直角三角形的边长为x,$\frac{ax}{b}$,$\frac{ax}{c}$,所以y=$\frac{{a}^{2}c}{{a}^{2}b+a{c}^{2}}$x
同样,设第三个正方形边长为z 则有z=$\frac{{a}^{2}c}{{a}^{2}b+a{c}^{2}}$y,
所以zx=y2,从而证明了x,y,z为等比数列,
所以其内接圆半径也是等比数列,即r1r3=r${\;}_{2}^{2}$.
点评 本题考查三角形相似的判定与性质,考查学生分析解决问题的能力,确定三个正方形的边长为等比数列是关键.

练习册系列答案
相关题目
9.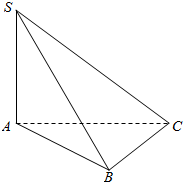 如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
 如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )| A. | $\frac{3a}{2}$ | B. | $\frac{2\sqrt{21}}{7}$a | C. | $\frac{5a}{2}$ | D. | $\frac{7a}{2}$ |
6.下列说法错误的是( )
| A. | 若棱柱的底面边长相等,则它的各个侧面的面积相等 | |
| B. | 九棱柱有9条侧棱,9个侧面,侧面为平行四边形 | |
| C. | 六角螺帽、三棱镜的外形都是棱柱 | |
| D. | 正四棱台的侧面不一定是等腰梯形 |
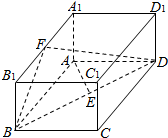 如图,已知在长方体ABCD-A1B1C1D1中,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.
如图,已知在长方体ABCD-A1B1C1D1中,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.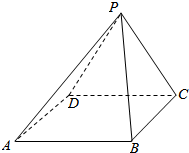 在正四棱锥P-ABCD中,AB=2.
在正四棱锥P-ABCD中,AB=2.
 在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC
在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC