题目内容
自A(4,0)引圆x2+y2=4的割线ABC,求弦BC中点P的轨迹方程.
BC中点P的轨迹方程为x2+y2-4x=0(在已知圆内的部分).
设P(x,y),连结OP,则OP⊥BC,
当x≠0时,kOP·kAP=-1,
即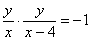 ,
,
即x2+y2-4x=0.①
当x=0时,P点坐标(0,0)是方程①的解,
∴BC中点P的轨迹方程为x2+y2-4x=0(在已知圆内的部分).
当x≠0时,kOP·kAP=-1,
即
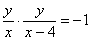 ,
,即x2+y2-4x=0.①
当x=0时,P点坐标(0,0)是方程①的解,
∴BC中点P的轨迹方程为x2+y2-4x=0(在已知圆内的部分).

练习册系列答案
相关题目
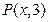 向圆
向圆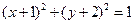 引切线,则切线长度的最小值等于( ).
引切线,则切线长度的最小值等于( ).



 ,求圆心到直线
,求圆心到直线 的距离的取值范围.(14分)
的距离的取值范围.(14分) 被圆
被圆 所截得的弦长等于
所截得的弦长等于 ,则
,则 的值为 ( )
的值为 ( ) 






