题目内容
求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且满足下列条件之一的圆的方程.
(1)过原点;
(2)有最小面积.
(1)过原点;
(2)有最小面积.
(1)过原点圆的方程为 .
.
(2)有最小面积 圆的方程为 .
.
 .
. (2)有最小面积 圆的方程为
 .
.设所求圆的方程为
x2+y2+2x-4y+1+λ(2x+y+4)=0,
即x2+y2+2(1+λ)x+(λ-4)y+(1+4λ)=0.
(1)因为此圆过原点,
∴1+4λ=0, .
.
故所求圆的方程为 .
.
(2)当半径最小时,圆面积也最小,
对圆的方程左边配方得
 ,
,
∴当 时,此圆面积最小,
时,此圆面积最小,
故满足条件的圆的方程为 .
.
x2+y2+2x-4y+1+λ(2x+y+4)=0,
即x2+y2+2(1+λ)x+(λ-4)y+(1+4λ)=0.
(1)因为此圆过原点,
∴1+4λ=0,
 .
.故所求圆的方程为
 .
.(2)当半径最小时,圆面积也最小,
对圆的方程左边配方得
 ,
,∴当
 时,此圆面积最小,
时,此圆面积最小,故满足条件的圆的方程为
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 AC切⊙O于点A,且
AC切⊙O于点A,且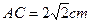 ,过C的割线CMN交
,过C的割线CMN交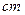 .
.