题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)证明![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(2)求![]() ;
;
(3)设![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)设![]() ,将已知条件中的式子进行转化,可得
,将已知条件中的式子进行转化,可得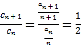 ,从而证得其为等比数列,之后利用等比数列的通项公式求得
,从而证得其为等比数列,之后利用等比数列的通项公式求得![]() ,进而求得
,进而求得![]() ;
;
(2)利用错位相减法对数列求和,求得![]() ;
;
(3)根据题意求得![]() ,将恒成立转化为
,将恒成立转化为![]() ,利用作差比较法,求得
,利用作差比较法,求得![]() ,观察得出
,观察得出![]() ,进而求得
,进而求得![]() 的范围.
的范围.
(1)设![]() ,则只需证明
,则只需证明![]() 为等比数列即可,
为等比数列即可,
因为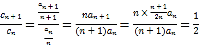 为常数,
为常数,
所以数列![]() 是公比为
是公比为![]() 的等比数列,且首项
的等比数列,且首项![]() ,
,
则![]() ,所以
,所以![]() .
.
(2)由(1)知![]() ①
①
![]() ②
②
①-②得,![]()
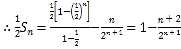
![]()
(3)由(2)得,![]() ,
,
要使得![]() 对
对![]() 恒成立,只需
恒成立,只需![]() ,
,
因为![]() ,
,
所以,当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() .
.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
【题目】某社区为了解居民喜欢中华传统文化是否与年龄有关,随机调查了60位居民,相关数据统计如下表所示,
喜欢 | 不喜欢 | 合计 | |
大于45岁 | 26 | 6 | 32 |
25岁至45岁 | 13 | 15 | 28 |
合计 | 39 | 21 | 60 |
(Ⅰ)是否有99.5%以上的人把握认为喜欢中华传统文化与年龄有关?
(Ⅱ)按年龄采用分层抽样的方法从喜欢中华传统文化的受调查居民中随机抽取6人作进一步了解,若从这6位居民中任选2人,求这2人的年龄均大于45岁的概率.
附:![]()
![]()
| 0.025 | 0.010 | 0.005 | 0,001 |
| 5.024 | 6.635 | 7.879 | 10.828 |