题目内容
2.已知函数f(x)=|2x-a|+a.(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值.
(2)在(1)的条件下,若存在实数n使f($\frac{1}{2}$n)≤m-f(-n)成立,求实数m的取值范围.
分析 (1)原不等式可化为|2x-a|≤6-a,解得a-3≤x≤3.再根据不等式f(x)≤6的解集为[-2,3],可得a-3=-2,从而求得a的值.
(2)由题意可得|n-1|+|2n-1|+2≤m,构造函数y=|n-1|+|2n-1|+2,求得y的最小值,从而求得m的范围.
解答 解:(1)原不等式可化为|2x-a|≤6-a,
∴$\left\{\begin{array}{l}6-a≥0\\ a-6≤2x-a≤6-a\end{array}\right.$,
解得a-3≤x≤3.
再根据不等式f(x)≤6的解集为[-2,3],可得a-3=-2,
∴a=1.
(2)∵f(x)=|2x-1|+1,f($\frac{1}{2}$n)≤m-f(-n),
∴|n-1|+1≤m-(|-2n-1|+1),
∴|n-1|+|2n+1|+2≤m,
∵y=|n-1|+|2n+1|+2,
当n≤-$\frac{1}{2}$时,y=-3n+2≥$\frac{7}{2}$,
当-$\frac{1}{2}$≤n≤1时,y=n+2≥$\frac{5}{2}$,
当n≥1时,y=3n≥3,
故函数y=|n-1|+|2n-1|+2的最小值为$\frac{5}{2}$,
∴m≥$\frac{5}{2}$,
即m的范围是[$\frac{5}{2}$,+∞).
点评 本题主要考查绝对值不等式的解法,带有绝对值的函数,体现了转化的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,可见部分信息如下,据此计算得到:参加数学抽测的人数n、分数在[90,100]内的人数分别为( )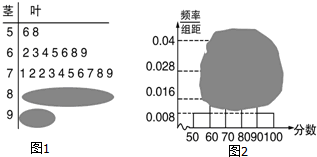

| A. | 25,2 | B. | 25,4 | C. | 24,2 | D. | 24,4 |
11. 执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
 执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |