题目内容
14．函数y=2x+$\frac{1}{x}$（x＞0）的最小值是2$\sqrt{2}$，此时x=$\frac{\sqrt{2}}{2}$．分析 根据基本不等式的性质进行计算即可．
解答 解：y≥2$\sqrt{2x•\frac{1}{x}}$=2$\sqrt{2}$，
当且仅当：2x=$\frac{1}{x}$，即x=$\frac{\sqrt{2}}{2}$时“=”成立，
故答案为：$2\sqrt{2}$，$\frac{{\sqrt{2}}}{2}$．
点评 本题考查了基本不等式的性质的应用，注意满足3个条件：一正二定三相等，本题是一道基础题．
练习册系列答案
相关题目
9．已知$\overrightarrow{a}$=（2，0），$\overrightarrow{b}$=（1，1），则下列结论正确的是（ ）
| A． | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B． | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | C． | $\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直 | D． | $\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$ |
6．
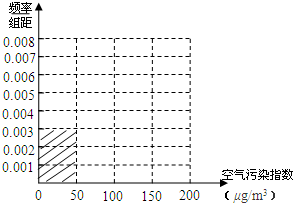当空气污染指数（单位：μg/m3）为0～50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为200～300时，空气质量级别为五级，空气质量状况属于重度污染；当空气污染指数为300以上时，空气质量级别为六级，空气质量状况属于严重污染．某日某省x个监测点数据统计如下：
（1）根据所给统计表和频率分布直方图中的信息求出x，y的值，并完成频率分布直方图；
（2）若A市共有5个监测点，其中有3个监测点为轻度污染，2个监测点为良．从中任意选取2个监测点，事件A“其中至少有一个为良”发生的概率是多少？
当空气污染指数（单位：μg/m3）为0～50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为200～300时，空气质量级别为五级，空气质量状况属于重度污染；当空气污染指数为300以上时，空气质量级别为六级，空气质量状况属于严重污染．某日某省x个监测点数据统计如下：| 空气污染指数（单位：μg/m3） | [0，50] | （50，100] | （100，150] | （150，200] |
| 监测点个数 | 15 | 40 | y | 10 |
（2）若A市共有5个监测点，其中有3个监测点为轻度污染，2个监测点为良．从中任意选取2个监测点，事件A“其中至少有一个为良”发生的概率是多少？