题目内容
定义函数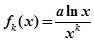 为
为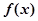 的
的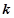 阶函数.
阶函数.
(1)求一阶函数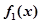 的单调区间;
的单调区间;
(2)讨论方程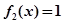 的解的个数;
的解的个数;
(3)求证: .
.
(1)当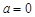 时,
时,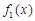 无单调区间;
无单调区间;
当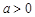 时,
时,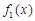 的单增区间为
的单增区间为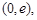 单减区间为
单减区间为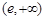 ;
;
当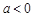 时,
时,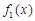 的单增区间为
的单增区间为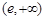 ,单减区间为
,单减区间为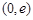 ;
;
(2)当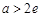 时,方程有两个不同解.当
时,方程有两个不同解.当 时,方程有0个解.当
时,方程有0个解.当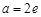 或
或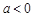 时,方程有唯一;
时,方程有唯一;
(3)详见解析.
解析试题分析:(1)求导,对 分情况讨论;
分情况讨论;
(2)研究方程的解的个数,实质就是研究函数的图象.通过求导,弄清函数的单调区间及函数值的范围,结合图象即可知道方程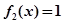 的解的个数.
的解的个数.
(3)待证不等式
可变为 ,左右对照,考虑证:
,左右对照,考虑证:
再联系到本题所给函数,可令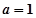 ,且研究
,且研究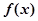 的3阶函数,即
的3阶函数,即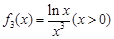 .
.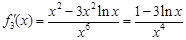 .由
.由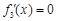 得
得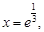
则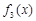 在
在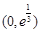 单调递增,在
单调递增,在 单调递减.
单调递减.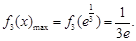
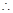
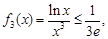 即
即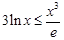 .又
.又 时,
时,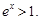
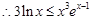
再令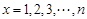 即得证.
即得证.
试题解析:(1)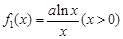 ,
,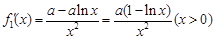
令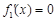 ,当
,当 时,
时,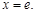
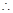 当
当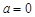 时,
时,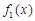 无单调区间;
无单调区间;
当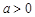 时,
时,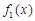 的单增区间为
的单增区间为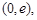 单减区间为
单减区间为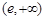 .
.
当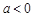 时,
时,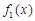 的单增区间为
的单增区间为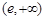 ,单减区间为
,单减区间为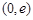 .
.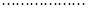 4分.
4分.
(2)由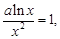 当
当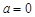 时,方程无解.当
时,方程无解.当 时,
时,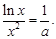
令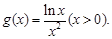 则
则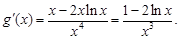 由
由 得
得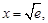
从而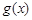 在
在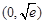 单调递增,在
单调递增,在 单调递减.
单调递减.
当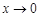 时,
时,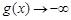 ,当
,当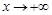
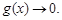
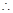 当
当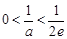 ,即
,即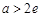 时,方程有两个不同解.
时,方程有两个不同解.
当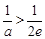 ,即
,即 时,方程有0个解
时,方程有0个解
当 ,
, 或即
或即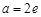 或
或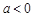 时,方程有唯一解.
时,方程有唯一解.
综上,当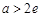 时,方程有两个不同解.当
时,方程有两个不同解.当 时,方程有0个解.当
时,方程有0个解.当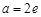 或
或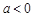 时,方程有唯一解. 9分.
时,方程有唯一解. 9分.
(3)特别地:当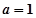 时由
时由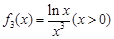 得
得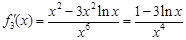 .
.
由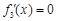 得
得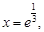
则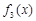 在
在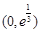 单调递增,在
单调递增,在 单调递减.
单调递减.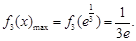
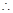

练习册系列答案
相关题目
 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 ),
), (单位:弧度).
(单位:弧度).
 的函数;
的函数; 的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设
的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设 .
.
 (O为坐标原点)的面积S表示成f的函数S(t);
(O为坐标原点)的面积S表示成f的函数S(t); ,S(t)取得最小值,求此时a的值及S(t)的最小值.
,S(t)取得最小值,求此时a的值及S(t)的最小值. (其中
(其中 为常数).
为常数).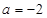 时,求函数
时,求函数 的最值;
的最值;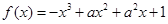 (
(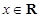 ),其中
),其中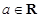 .
.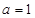 时,求曲线
时,求曲线 在点
在点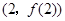 处的切线方程;
处的切线方程;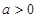 时,求函数
时,求函数 的极大值和极小值.
的极大值和极小值. ,
, .
. ,求证:当
,求证:当 时,
时, ;
; 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围; .
.

 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 时,求函数
时,求函数 的极值;
的极值; ,
, 的三个顶点
的三个顶点 在函数
在函数 ,
, 、
、 、
、 分别为
分别为