题目内容
已知函数 (其中
(其中 为常数).
为常数).
(I)当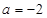 时,求函数
时,求函数 的最值;
的最值;
(Ⅱ)讨论函数 的单调性.
的单调性.
(I)当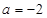 时,函数
时,函数 的最小值为
的最小值为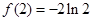 ,
, 无最大值;(Ⅱ)当
无最大值;(Ⅱ)当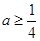 时,
时, 在区间
在区间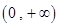 上单调递增;当
上单调递增;当 时,
时, 在区间
在区间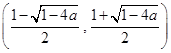 上单调递减,在区间
上单调递减,在区间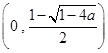 和
和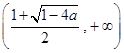 上单调递增;当
上单调递增;当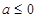 时,
时, 在区间
在区间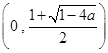 上单调递减;在区间
上单调递减;在区间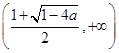 上单调递增.
上单调递增.
解析试题分析:(I)由已知条件,写出当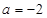 时,函数
时,函数 的解析式,先求函数
的解析式,先求函数 的定义域,再求函数
的定义域,再求函数 的导数,令
的导数,令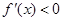 和
和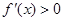 ,分别求出函数的单调增区间和单调减区间,最后可求得
,分别求出函数的单调增区间和单调减区间,最后可求得 函数的最值;(Ⅱ)先求出函数
函数的最值;(Ⅱ)先求出函数 的导数:
的导数: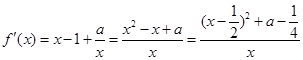 ,再观察发现,当
,再观察发现,当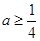 时,
时,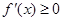 恒成立,
恒成立, 在区间
在区间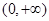 上单调递增.当
上单调递增.当 时,由
时,由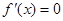 ,得
,得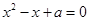 ,解这个方程,讨论可得函数
,解这个方程,讨论可得函数 的单调性.
的单调性.
试题解析:(I) 的定义域为
的定义域为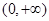 ,当
,当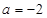 时,
时,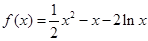 ,
,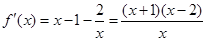 . 2分
. 2分
由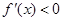 ,得
,得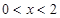 ,由
,由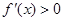 ,得
,得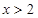 ,
, 在区间
在区间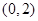 上单调递减,
上单调递减,
在区间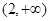 上单调递增,故当
上单调递增,故当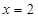 时,
时, 取最小值
取最小值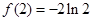 ,
, 无最大值. 4分
无最大值. 4分
(Ⅱ)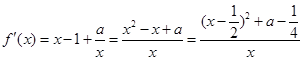 . 5分
. 5分
当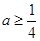 时,
时,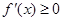 恒成立,
恒成立, 在区间
在区间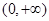 上单调递增; 6分
上单调递增; 6分
当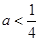 时,由
时,由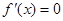 得
得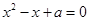 ,解得
,解得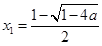 ,
,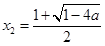 . 7分
. 7分
当 时,
时, ,由
,由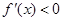 得
得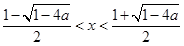 ,
, 在区间
在区间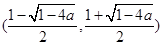 上单调递减,
上单调递减,
在区间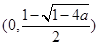 和
和 上单调递增 9分
上单调递增 9分
当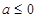 时,
时,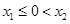 ,由
,由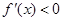 得
得 ,
, 在区间
在区间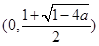 上单调递减;在区间
上单调递减;在区间 上单调递增.
上单调递增.
综上,当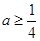 时,
时, 在区间
在区间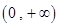 上单调递增;当
上单调递增;当 时,
时, 在区间
在区间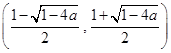 上单调递减,在区间
上单调递减,在区间
练习册系列答案
相关题目
 在x=0,x=
在x=0,x= 处存在极值。
处存在极值。 ,
, ,其中
,其中 且
且 .
.  ,求函数
,求函数 的单调递增区间;
的单调递增区间; 时,函数
时,函数 有极值,求函数
有极值,求函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由. 为
为 的
的 阶函数.
阶函数. 的单调区间;
的单调区间; 的解的个数;
的解的个数; .
.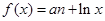 ,其中实数a为常数.
,其中实数a为常数. 的单调区间:
的单调区间: (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值; .
.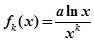 为
为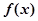 的
的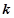 阶函数.
阶函数.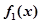 的单调区间;
的单调区间;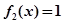 的解的个数;
的解的个数; .
. 的图象在
的图象在 上连续,定义:
上连续,定义: ,
,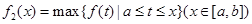 .其中,
.其中, 表示函数
表示函数 上的最小值,
上的最小值, 表示函数
表示函数 ,使得
,使得 对任意的
对任意的 成立,则称函数
成立,则称函数 ,试写出
,试写出 ,
, 的表达式;
的表达式; ,试判断
,试判断 上的“
上的“ ,函数
,函数 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围. ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线垂直于
处的切线垂直于 轴.
轴. 的值;
的值; 的极值.
的极值.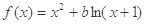 ,其中
,其中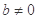 .
.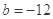 ,求
,求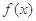 在
在 的最小值;
的最小值;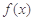 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数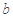 的取值范围;
的取值范围;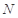 ,使得当
,使得当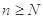 时,不等式
时,不等式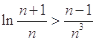 恒成立.
恒成立.