题目内容
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施不能建设开发,且要求用栏栅隔开(栏栅要求在直线上),公共设施边界为曲线 的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设
的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设 .
.
(I)将 (O为坐标原点)的面积S表示成f的函数S(t);
(O为坐标原点)的面积S表示成f的函数S(t);
(II)若 ,S(t)取得最小值,求此时a的值及S(t)的最小值.
,S(t)取得最小值,求此时a的值及S(t)的最小值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)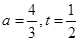 时,
时,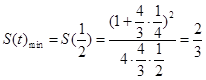 .
.
解析试题分析:(Ⅰ)根据导数的几何意义,直线 的斜率为
的斜率为 在
在 的导函数值
的导函数值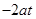 ,从而得到直线
,从而得到直线 的方程为
的方程为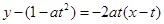 ;进一步通过确定纵、横截距,计算三角形的面积.
;进一步通过确定纵、横截距,计算三角形的面积.
(Ⅱ)应用导数研究函数的最值,遵循“求导数,求驻点,讨论导函数的正负,确定最值”. 注意到本题驻点唯一,其必是“最值点”.
试题解析:Ⅰ) ,直线
,直线 的斜率为
的斜率为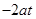 ,
,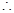 直线
直线 的方程为
的方程为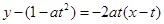
令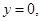 得
得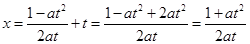
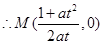 3分
3分
令 ,得
,得 ,
,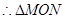 的面积
的面积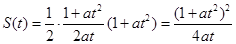 , 6分
, 6分
(Ⅱ)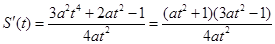 ,
,
因为 ,由
,由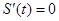 ,得
,得 , 9分
, 9分
当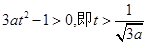 时,
时,  ,
,
当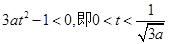 时,
时, 
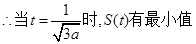 .
.
已知在 处,
处, 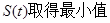 ,故有
,故有 ,
,
故当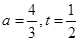 时,
时,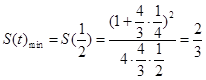 13分
13分
考点:生活中的优化问题举例,导数的几何意义,直线方程,应用导数研究函数的最值.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 处的切线与直线
处的切线与直线 平行.
平行. 在区间
在区间 内有两个不等的实数根?
内有两个不等的实数根? ,其中
,其中 为常数.
为常数. 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; ,求函数
,求函数 上是增函数的概率.
上是增函数的概率.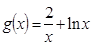 ,
,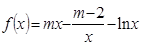 ,
,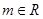 .
.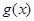 的极值点;
的极值点;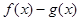 在
在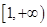 上为单调函数,求
上为单调函数,求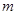 的取值范围;
的取值范围;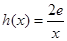 ,若在
,若在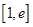 上至少存在一个
上至少存在一个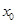 ,使得
,使得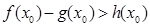 成立,求
成立,求 为
为 的
的 阶函数.
阶函数. 的单调区间;
的单调区间; 的解的个数;
的解的个数; .
.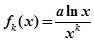 为
为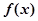 的
的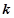 阶函数.
阶函数.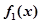 的单调区间;
的单调区间;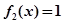 的解的个数;
的解的个数; .
.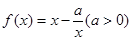 ,
,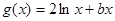 ,且直线
,且直线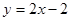 与曲线
与曲线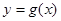 相切.
相切.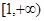 内的一切实数
内的一切实数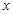 ,不等式
,不等式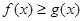 恒成立,求实数
恒成立,求实数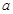 的取值范围;
的取值范围;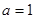 时,求最大的正整数
时,求最大的正整数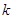 ,使得任意
,使得任意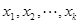
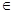
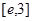 (
(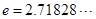 是自然对数的底数)都有
是自然对数的底数)都有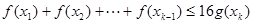 成立;
成立;
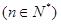 .
.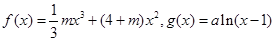 ,其中
,其中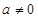 .
.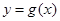 图象恒过定点P,且点P关于直线
图象恒过定点P,且点P关于直线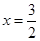 的对称点在
的对称点在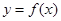 的图象上,求m的值;
的图象上,求m的值;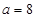 时,设
时,设 ,讨论
,讨论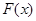 的单调性;
的单调性;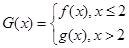 ,曲线
,曲线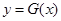 上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.