题目内容
17．在△ABC中，A=60°，AC=2，BC=$\sqrt{3}$，则AB等于1．分析 由已知及正弦定理可得sinB=$\frac{AC•sinA}{BC}$=1，结合B为三角形内角，可得B=90°，解得：C=30°，由余弦定理可求AB的值．
解答 解：∵A=60°，AC=2，BC=$\sqrt{3}$，
∴由正弦定理可得：sinB=$\frac{AC•sinA}{BC}$=$\frac{2×\frac{\sqrt{3}}{2}}{\sqrt{3}}$=1，
∴B为三角形内角，可得B=90°，解得：C=30°，
∴由余弦定理可得：AB=$\sqrt{A{C}^{2}+B{C}^{2}-2AC•BC•cosC}$=$\sqrt{4+3-2×2×\sqrt{3}×\frac{\sqrt{3}}{2}}$=1．
故答案为：1．
点评 本题主要考查了正弦定理，余弦定理，三角形内角和定理在解三角形中的应用，属于基础题．
练习册系列答案
相关题目
13．已知命题p：?x∈R，x-1＞lnx，命题q：函数y=ax+a-x（a＞1）在R上为减函数，则 （ ）
| A． | 命题p∨q是假命题 | B． | 命题p∧q是真命题 | ||
| C． | 命题p∧（-q）是真命题 | D． | 命题p∨（-q）是假命题 |
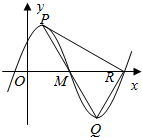如图是函数f（x）=Asin（ωx+φ）的部分图象，P、Q分别为该图象的最高点和最低点，R是该图象与x轴的一个交点，且PR⊥QR，△PQR的面积为2$\sqrt{3}$，则函数f（x）的最小正周期为4．