Question

12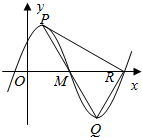．如图是函数f（x）=Asin（ωx+φ）的部分图象，P、Q分别为该图象的最高点和最低点，R是该图象与x轴的一个交点，且PR⊥QR，△PQR的面积为2$\sqrt{3}$，则函数f（x）的最小正周期为4．

Answer 1

分析 由题意可知△MQR是正三角形，设出其边长为a，把△PQR的面积用含有a的代数式表示并求得a，则答案可求．

解答 解：由图象的对称性可知，PQ=2QR，
又PR⊥QR，故∠QPR=30°，则△MQR是正三角形，
设MR=QR=a，则PR=$\sqrt{3}a$，
∴$\frac{1}{2}a•\sqrt{3}a=2\sqrt{3}$，解得a=2．
∴最小正周期T=2a=4．
故答案为：4．

点评 本题考查f（x）=Asin（ωx+φ）型函数的图象和性质，关键是把△PQR的面积用正三角形MQR的边长表示，是基础的计算题．