题目内容
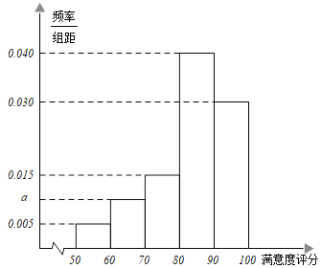
【题目】为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的 500 名志愿者中随机抽取 100 名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是[20,25),[25,30),[30,35),[35,40),[40,45].
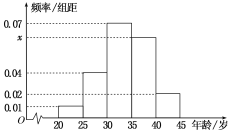
(1)求图中x的值并根据频率分布直方图估计这 500 名志愿者中年龄在[35,40)岁的人数;
(2)在抽出的 100 名志愿者中按年龄采用分层抽样的方法抽取 20 名参加中心广场的宣传活动,再从这 20 名中采用简单随机抽样方法选取 3 名志愿者担任主要负责人.记这 3 名志愿者中“年龄低于 35 岁”的人数为 X,求 X 的分布列及均值.
【答案】(1)![]() (2)
(2)
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]()
【解析】
![]() 根据频率分布直方图中矩形面积之和为
根据频率分布直方图中矩形面积之和为![]() 可以计算出
可以计算出![]() 的值,再利用相应公式计算出相应组中抽取的人数
的值,再利用相应公式计算出相应组中抽取的人数
![]() 先确定“低于
先确定“低于![]() 岁”和“年龄不低于
岁”和“年龄不低于![]() 岁”相应的人数,然后利用排列组合计算即可得到答案
岁”相应的人数,然后利用排列组合计算即可得到答案
(1)∵小矩形的面积等于频率,∴除[35,40)外的频率和为0.70,![]()
故500 名志愿者中,年龄在[35,40)岁的人数为 0.06×5×500=150(人).
(2)用分层抽样的方法,从中选取 20 名,则其中年龄“低于 35 岁”的人有12 名,“年龄不低于 35 岁”的人有 8 名.
故 ![]() 的可能取值为 0,1,2,3,
的可能取值为 0,1,2,3,
![]() ,
,![]()
![]() ,
,![]() ,
,
故 X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
则![]()

【题目】![]() 大学就业指导中心对该校毕业生就业情况进行跟踪调查,发现不同的学历对就业专业是否为毕业所学专业有影响,就业指导中心从
大学就业指导中心对该校毕业生就业情况进行跟踪调查,发现不同的学历对就业专业是否为毕业所学专业有影响,就业指导中心从![]() 届的毕业生中,抽取了本科和研究生毕业生各
届的毕业生中,抽取了本科和研究生毕业生各![]() 名,得到下表中的数据.
名,得到下表中的数据.
就业专业 毕业学历 | 就业为所学专业 | 就业非所学专业 |
本科 |
|
|
研究生 |
|
|
(1)根据表中的数据,能否在犯错概率不超过![]() 的前提下认为就业专业是否为毕业所学专业与毕业生学历有关;
的前提下认为就业专业是否为毕业所学专业与毕业生学历有关;
(2)为了进一步分析和了解本科毕业生就业的问题,按分层抽样的原则从本科毕业生中抽取一个容量为![]() 的样本,要从
的样本,要从![]() 人中任取
人中任取![]() 人参加座谈,求被选取的
人参加座谈,求被选取的![]() 人中至少有
人中至少有![]() 人就业非毕业所学专业的概率.
人就业非毕业所学专业的概率.
附: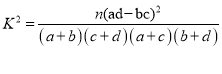 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|