Question

【题目】已知函数，给出下列结论：

①的单调递减区间；

②当时，直线y=k与y=f （x）的图象有两个不同交点；

③函数y=f（x）的图象与的图象没有公共点；

④当时，函数的最小值为2．

其中正确结论的序号是_________

Answer 1

【答案】①③

【解析】

①先求出函数的导数，令导函数小于0，解出即可判断；②根据函数的单调性画出函数的图象，通过图象读出即可；③求出f（x）的最大值小于y＝x2+1的最小值，从而得到答案；④利用对勾函数即可作出判断．

解：①f′（x），令f′（x）＜0，解得：x＞1，

∴函数f（x）在（1，+∞）递减，故①正确；

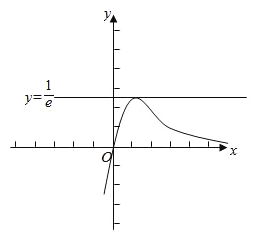
②∵f（x）在（﹣∞，1）递增，在（1，+∞）递减，

∴f（x）max＝f（1），

x→﹣∞时，f（x）→﹣∞，x→+∞时，f（x）→0，

画出函数f（x）的图象，如图示：

，

∴当k∈（﹣∞，0）时，直线y＝k与y＝f（x）的图象有1个不同交点，

当k∈（0，）时，直线y＝k与y＝f（x）的图象有两个不同交点，故②错误；

③函数f（x），而y＝x2+1≥1，

∴函数y＝f（x）的图象与y＝x2+1的图象没有公共点，故③正确；

④当时，令t=，

在上单调递减，

∴，最小值不等于2，故④错误.

故答案为：①③．