题目内容
【题目】已知椭圆![]()
![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上.
上.
(I)求椭圆![]() 的标准方程;
的标准方程;
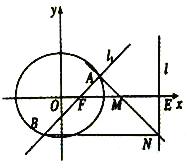
(Ⅱ)过![]() 的右焦点
的右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 为线段
为线段![]() 的中点,过点
的中点,过点![]() 作直线
作直线![]() 于点
于点![]() .证明:
.证明:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
【答案】(I)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
(I)根据椭圆的对称性,得到![]() ,
,![]() 在椭圆
在椭圆![]() 上,
上,![]() 不在椭圆
不在椭圆![]() 上,将点
上,将点![]() ,
,![]() 代入椭圆
代入椭圆![]() 的方程,联立得到
的方程,联立得到![]() ,
,![]() ,即可求出椭圆
,即可求出椭圆![]() 方程。
方程。
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,由于
,代入椭圆方程,由于![]() 为线段
为线段![]() 的中点、直线
的中点、直线![]() 于点
于点![]() ,所以点
,所以点![]() 、点
、点![]() ,分别得到
,分别得到![]() 、
、![]() 的表达式,然后相减检验是否为0,若为0,即三点共线。
的表达式,然后相减检验是否为0,若为0,即三点共线。
(I)根据椭圆对称性,必过![]() ,
,![]() ,又
,又![]() ,
,![]() 不在
不在![]() 上,
上,
∴ 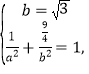 ∴
∴ ![]() ,
,![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
代入椭圆方程,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
易知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() 三点共线.
三点共线.

练习册系列答案
相关题目
【题目】为了解人们对“延迟退休年龄政策”的态度,某部门从年龄在![]() 岁到
岁到![]() 岁的人群中随机调查了
岁的人群中随机调查了![]() 人,并得到如图所示的频率分布直方图,在这
人,并得到如图所示的频率分布直方图,在这![]() 人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如图所示:
人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如图所示:

年龄 | 不支持“延迟退休年龄政策”的人数 |
|
|
|
|
|
|
|
|
|
|
(1)由频率分布直方图,估计这![]() 人年龄的平均数;
人年龄的平均数;
(2)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以
的前提下,认为以![]() 岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
45岁以下 | 45岁以上 | 总计 | |
不支持 | |||
支持 | |||
总计 |
附:![]()
参考数据:
|
|
|
|
|
|
|
|
|
|