题目内容
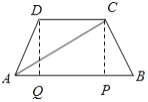
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() .
.
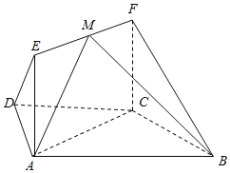
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的平面角为
所成锐二面角的平面角为![]() ,且满足
,且满足![]() ?若不存在,请说明理由;若存在,求出
?若不存在,请说明理由;若存在,求出![]() 的长度.
的长度.
【答案】(1)见解析(2)在线段![]() 上存在点
上存在点![]() 满足题意,
满足题意,![]() .
.
【解析】
(1)如图所示的等腰梯形![]() 中,经过点
中,经过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,垂足为
,垂足为![]() .利用矩形的性质可求出
.利用矩形的性质可求出![]() ,在
,在![]() 中,利用余弦定理可得
中,利用余弦定理可得![]() ,利用勾股定理的逆定理可得
,利用勾股定理的逆定理可得![]() ,再利用面面垂直的性质定理即可证明
,再利用面面垂直的性质定理即可证明![]() 平面
平面![]() ;
;
(2)如图所示,建立空间直角坐标系.设![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,可得
,可得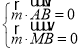 ,取平面
,取平面![]() 的法向量
的法向量![]() ,利用
,利用![]() ,
,![]() ,即可求出.
,即可求出.
(1)如图所示的等腰梯形![]() 中,经过点
中,经过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,垂足为
,垂足为![]() ,则
,则![]() 为矩形,
为矩形,![]() .在
.在![]() 中,
中,![]() ,则
,则![]() ,
,
同理可得![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又∵四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
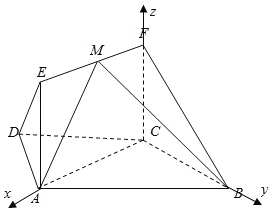
(2)如图所示,建立空间直角坐标系.
![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,
![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则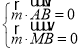 ,∴
,∴ 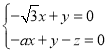
取![]() .
.
取平面![]() 的法向量
的法向量![]() .
.
由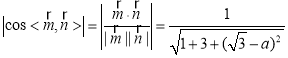 ,
,
由题意可得: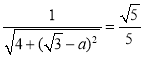 ,
,![]() .
.
解得![]() .
.
因此在线段![]() 上点
上点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的平面角为
所成锐二面角的平面角为![]() ,且满足
,且满足![]() ,
,![]() .
.

【题目】一项针对都市熟男(三线以上城市,![]() 岁男性)消费水平的调查显示,对于最近一年内是否购买过以下七类高价商品,全体被调查者,以及其中包括的1980年及以后出生(80后)被调查者,1980年以前出生(80前)被调查者回答“是”的比例分别如下:
岁男性)消费水平的调查显示,对于最近一年内是否购买过以下七类高价商品,全体被调查者,以及其中包括的1980年及以后出生(80后)被调查者,1980年以前出生(80前)被调查者回答“是”的比例分别如下:
全体被调查者 | 80后被调查者 | 80前被调查者 | |
电子产品 | 56.9% | 66.0% | 48.5% |
服装 | 23.0% | 24.9% | 21.2% |
手表 | 14.3% | 19.4% | 9.7% |
运动、户外用品 | 10.4% | 11.1% | 9.7% |
珠宝首饰 | 8.6% | 10.8% | 6.5% |
箱包 | 8.1% | 11.3% | 5.1% |
个护与化妆品 | 6.6% | 6.0% | 7.2% |
以上皆无 | 25.3% | 17.9% | 32.1% |
根据表格中数据判断,以下分析错误的是( )
A. 都市熟男购买比例最高的高价商品是电子产品
B. 从整体上看,80后购买高价商品的意愿高于80前
C. 80前超过3成一年内从未购买过表格中七类高价商品
D. 被调查的都市熟男中80后人数与80前人数的比例大约为![]()
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | |
直径/mm | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(I)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行判定(
,并根据以下不等式进行判定(![]() 表示相应事件的概率):①
表示相应事件的概率):①![]() ;②
;②![]() ;③
;③![]() .判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁.试判断设备
.判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁.试判断设备![]() 的性能等级.
的性能等级.
(Ⅱ)将直径尺寸在![]() 之外的零件认定为是“次品”,将直径尺寸在
之外的零件认定为是“次品”,将直径尺寸在![]() 之外的零件认定为“突变品”.从样本的“次品”中随意抽取两件,求至少有一件“突变品”的概率.
之外的零件认定为“突变品”.从样本的“次品”中随意抽取两件,求至少有一件“突变品”的概率.