题目内容
4. 如图,已知点S(-2,0)和圆O:x2+y2=4,ST是圆O的直径,从左到右M、O和N依次是ST的四等分点,P(异于S,T)是圆O上的动点,PD⊥ST,交ST于D,$\overrightarrow{PE}$=λ$\overrightarrow{ED}$,直线PS与TE交于C,|CM|+|CN|为定值.
如图,已知点S(-2,0)和圆O:x2+y2=4,ST是圆O的直径,从左到右M、O和N依次是ST的四等分点,P(异于S,T)是圆O上的动点,PD⊥ST,交ST于D,$\overrightarrow{PE}$=λ$\overrightarrow{ED}$,直线PS与TE交于C,|CM|+|CN|为定值.(1)求点C的轨迹曲线Γ的方程及λ的值;
(2)设n是过原点的直线,直线l与n垂直相交于Q点,l与轨迹Γ相交于A,B两点,且|$\overrightarrow{OQ}$|=1.是否存在直线l,使$\overrightarrow{AQ}$•$\overrightarrow{QB}$=1成立?若存在,求出直线l的方程;若不存在,请说明理由.
分析 (1)设出点的坐标,得$\frac{{y}^{2}}{{x}^{2}-4}=\frac{\frac{{{y}_{0}}^{2}}{1+λ}}{{{x}_{0}}^{2}-4}$,根据|CM|+|CN|为定值,建立条件关系即可求λ的值及点C的轨迹曲线E的方程;
(2)分类讨论,根据$\overrightarrow{AQ}$•$\overrightarrow{QB}$=1,|$\overrightarrow{OQ}$|=1,进行转化,将y=kx+m代入椭圆方程,利用x1x2+y1y2=0,即可得出结论.
解答 解:(1)由题意,T(2,0),M(-1,0),N(1,0),
设P(x0,y0),C(x,y),则E(x0,$\frac{{y}_{0}}{1+λ}$),
直线PS与TE交于C,故x≠±2,
$\frac{y}{x+2}=\frac{{y}_{0}}{{x}_{0}+2}$①且$\frac{y}{x-2}=\frac{\frac{{y}_{0}}{1+λ}}{{x}_{0}-2}$,②
①②相乘得$\frac{{y}^{2}}{{x}^{2}-4}=\frac{\frac{{{y}_{0}}^{2}}{1+λ}}{{{x}_{0}}^{2}-4}$,
又点P是圆O上的动点,故$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{\frac{4}{1+λ}}=1$,(4分)
要使|CM|+|CN|为定值,则4-$\frac{4}{1+λ}$=1,解得λ=$\frac{1}{3}$.
此时$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$(x≠±2).
即λ=$\frac{1}{3}$时,点C的轨迹曲线E的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$(x≠±2).
(2)设A,B两点的坐标分别为(x1,y1),(x2,y2),假设使$\overrightarrow{AQ}$•$\overrightarrow{QB}$=1成立的直线l存在,
(ⅰ)当l不垂直于x轴时,设l的方程为y=kx+m,
由l与n垂直相交于Q点且|$\overrightarrow{OQ}$|=1.得$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,即m2=k2+1
∵$\overrightarrow{AQ}$•$\overrightarrow{QB}$=1,|$\overrightarrow{OQ}$|=1.
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=($\overrightarrow{OQ}$+$\overrightarrow{QA}$)•($\overrightarrow{OQ}$+$\overrightarrow{QB}$)=0
即x1x2+y1y2=0,
将y=kx+m代入椭圆方程,得(3+4k2)x2+8kmx+(4m2-12)=0
由求根公式可得x1+x2=-$\frac{8km}{3+4{k}^{2}}$,④x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$ ⑤
0=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2,
将④,⑤代入上式并化简得 (1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0⑥
将m2=1+k2代入⑥并化简得-5(k2+1)=0,矛盾,即此时直线l不存在;
(ⅱ)当l垂直于x轴时,满足|$\overrightarrow{OQ}$|=1的直线l的方程为x=1或x=-1,
当X=1时,A,B,Q的坐标分别为(1,$\frac{3}{2}$),(1,-$\frac{3}{2}$),(1,0),
∴$\overrightarrow{AQ}$=(0,-$\frac{3}{2}$),$\overrightarrow{QB}$=(0,-$\frac{3}{2}$),
∴$\overrightarrow{AQ}$•$\overrightarrow{QB}$=$\frac{9}{4}$≠1
当x=-1时,同理可得$\overrightarrow{AQ}$•$\overrightarrow{QB}$≠1,矛盾,即此时直线l也不存在
综上可知,使$\overrightarrow{AQ}$•$\overrightarrow{QB}$=1成立的直线l不存在.
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

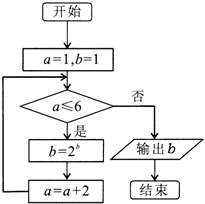
| A. | 4 | B. | 8 | C. | 16 | D. | 216 |
| A. | 1+2i | B. | i-1 | C. | 1-i | D. | 1-2i |

| A. | 16 | B. | 12 | C. | 8 | D. | 6 |
| A. | $\frac{8}{13}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{15}$ | D. | $\frac{8}{15}$ |
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别为PB,CD的中点,二面角P-CD-A的大小为60°,AC=AD=$\sqrt{2}$,CD=PN=2,PC=PD. 如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.
如图:在三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=2$\sqrt{11}$,点P在平面ABC内的射影恰为△ABC的重心G,M为侧棱AP上一动点.